
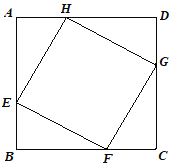
【题目】如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH.则四边形EFGH面积的最小值是________cm2.
【答案】32
【解析】分析:根据正方形的性质结合已知可推出:△EAH≌△FBE≌△GCF≌△HDG,结合全等三角形的性质得到四边形EFGH是菱形;根据角度间关系容易得出∠HEF=90°,进而得到四边形EFGH是正方形,设AE=DH=x,则AH=8-x,在Rt△AEH中利用勾股定理可得:EH2=AE2+AH2,结合二次函数的最值解答即可.
详解:∵四边形ABCD是正方形,
∴∠BAD=∠ABC=∠BCD=∠CDA=90°,AB=BC=CD=DA.
∵AE=BF=CG=DH,
∴BE=CF=AH=DG,
∴△EAH≌△FBE≌△GCF≌△HDG,
∴EH=EF=FG=HG,∠AEH=∠BFE,
∴四边形EFGH是菱形.
∵∠BEF+∠BFE=90°,∠AEH=∠BFE,
∴∠BEF+∠AEH=90°,
∴∠HEF=90°.
∵四边形EFGH是菱形,∠HEF=90°,
∴四边形EFGH是正方形.
正方形EFGH的面积最小,则边长EF最小.
设AE=DH=x,则AH=8-x,
∵在Rt△AEH中,EH2=AE2+AH2=x2+(8-x)2=2x2-16x+64=2(x-4)2+32,
∴四边形EFGH面积的最小值为32cm2.


科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数![]() ,B点示数
,B点示数![]() ,C点表示数
,C点表示数![]() ,
,![]() 是最小的正整数,且
是最小的正整数,且![]() 、
、![]() 满足
满足![]() .
.
![]()
(1)![]() =__________,
=__________,![]() =__________,
=__________,![]() =__________;
=__________;
(2)若将数轴折叠,使得A点与C点重合,则点B与数__________表示的点重合;
(3)若点A、点B和点C分别以每秒2个单位、1个单位长度和4个单位长度的速度在数轴上同时向左运动,假设![]() 秒钟过后,A、B、C三点中恰有一点为另外两点的中点,求
秒钟过后,A、B、C三点中恰有一点为另外两点的中点,求![]() 的值;
的值;
(4)若点A、点B和点C分别以每秒2个单位、1个单位长度和4个单位长度的速度在数轴上同时向左运动时,小聪同学发现:当点C在B点右侧时,![]() BC+3AB的值是个定值,求此时
BC+3AB的值是个定值,求此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
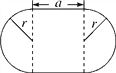
【题目】一个花坛的形状如图所示,它的两端是半径相等的半圆,求:
(1)花坛的周长l;
(2)花坛的面积S;
(3)若a=8m,r=5m,求此时花坛的周长及面积(π取3.14).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两城相距900千米,一辆客车从A城开往B城,车速为每小时80千米,同时一辆出租车从B城开往A城,车速为每小时100千米,设客车出发时间为t(小时).
探究 若客车、出租车距A城的距离分别为y1、y2,写出y1、y2关于t的函数关系式及自变量取值范围,并计算当y1=240千米时y2的値.
发现 (1)设点C是A城与B城的中点,AC=![]() AB,通过计算说明:哪个车先到达C城?该车到达C后再经过多少小时,另一个车会到达C?
AB,通过计算说明:哪个车先到达C城?该车到达C后再经过多少小时,另一个车会到达C?
(2)若两车扣相距100千米时,求时间t.
决策 已知客车和出租车正好在A,B之间的服务站D处相遇,此时出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种选择返回B城的方案:
方案一:继续乘坐出租车到C城,加油后立刻返回B城,出租车加油时间忽略不计;
方案二:在D处换乘客车返回B城.
试通过计算,分析小王选择哪种方式能更快到达B城?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组邻边相等的凸四边形叫做“准菱形”.利用该定义完成以下各题:
(1) 理解
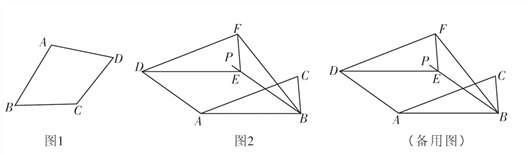
填空:如图1,在四边形ABCD中,若 (填一种情况),则四边形ABCD是“准菱形”;
(2)应用
证明:对角线相等且互相平分的“准菱形”是正方形;(请画出图形,写出已知,求证并证明)
(3) 拓展
如图2,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将Rt△ABC沿∠ABC的平分线BP方向平移得到△DEF,连接AD,BF,若平移后的四边形ABFD是“准菱形”,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 为有理数,定义一种新运算,其意义是
为有理数,定义一种新运算,其意义是![]()
![]() ,试根据这种运算完成下列各题
,试根据这种运算完成下列各题
(1)求①23;②(43)(-2)
(2)任意选择两个有理数,分别代替![]() 与
与![]() ,并比较
,并比较![]() 和
和![]() 两个运算的结果,你有何发现;
两个运算的结果,你有何发现;
(3)根据以上方法,探索![]() 的关系,并用等式把它们表示出来.
的关系,并用等式把它们表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:获利=售价-进价)

(1)若商店计划销售完这批商品后能获利1 100元,请问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并指出获利最大的购货方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com