练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

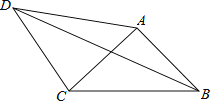
    【题目】如图，在四边形ABCD中，AD＝4，CD＝3，∠ABC＝∠ACB＝∠ADC＝45°，则BD的长为 .

    【答案】.

    【解析】

    试题根据等式的性质，可得∠BAD与∠CAD′的关系，根据SAS，可得△BAD与△CAD′的关系，根据全等三角形的性质，可得BD与CD′的关系，根据勾股定理，可得答案：

    如答图，作AD′⊥AD，AD′=AD，连接CD′，DD′，

    ∵∠ABC＝∠ACB＝45°，∴BA=BC.

    ∵∠BAC+∠CAD=∠DAD′+∠CAD，即∠BAD=∠CAD′，

    在△BAD与△CAD′中，∵，∴△BAD≌△CAD′（SAS）.∴BD=CD′．

    在Rt△ADD′中，由勾股定理得.

    ∵∠D′DA＝∠ADC＝45°，∴∠D′DC＝90°.

    在Rt△CDD′中，由勾股定理得，

    ∴BD=CD′=.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

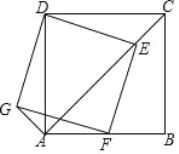
    【题目】如图，正方形ABCD中，AB＝4，点E是对角线AC上的一点，连接DE．过点E作EF⊥ED，交AB于点F，以DE、EF为邻边作矩 形DEFG，连接AG．

    （1）求证：矩形DEFG是正方形；

    （2）求AG+AE的值；

    （3）若F恰为AB中点，连接DF交AC于点M，求ME的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

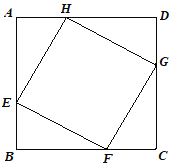
    【题目】如图，正方形ABCD的边长为8cm，E、F、G、H分别是AB、BC、CD、DA上的动点，且AE=BF=CG=DH．则四边形EFGH面积的最小值是________cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】做大小两个长方体纸盒，尺寸如下（单位：cm）

    长

    宽

    高

    小纸盒

    大纸盒

    (1) 做这两个纸盒共用料多少?

    (2) 做小纸盒比做大纸盒少用料多少

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程

    解:方程两边同时乘以(x+2)(x-2)…(A)

    (x+2)(x-2)

    化简得:x-2+4x=2(x+2)….. (B)

    去括号、移项得:x+4x-2x=4+2…(C)

    解得:x=2…..(D)

    原方程的解是x=2….(E)

    问题:①上述解题过程的错误在第____步,其原因是_____②该步改正为:

    查看答案和解析>>

    科目：初中数学 来源： 题型：

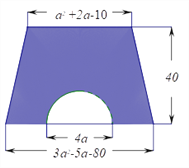
    【题目】如图，梯形的上底为+2-10，下底为3-5-80，高为40.（取3）

    （1）用式子表示图中阴影部分的面积；

    （2）当=10时，求阴影部分面积的值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知:如图,四边形ABCD是平行四边形,P是CD上的一点,且AP和BP分别分别平分∠DAB和∠CBA,QP∥AD,交AB于点Q.

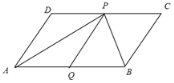
    (1)求证:AP⊥PB;

    (2)如果AD=5cm,AP=8cm,那么□ ABCD 的面积是多少?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知下列有理数：，－4，2.5，－1，0，3，，5

    （1）画数轴，并在数轴上表示这些数：

    （2）这些数中最小的数是________，指出这些数中互为相反数的两个数之间所有的整数共有________个

    （3）计算出，－4，2.5，－1，0，3，，5这些数的和的绝对值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，C是AB上一点，点D，E分别在AB两侧，AD∥BE，且AD＝BC，BE＝AC．

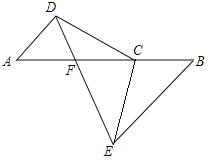
    （1）求证：CD＝CE；

    （2）连接DE，交AB于点F，猜想△BEF的形状，并给予证明．

    查看答案和解析>>

    同步练习册答案