
【题目】已知:如图,C是AB上一点,点D,E分别在AB两侧,AD∥BE,且AD=BC,BE=AC.
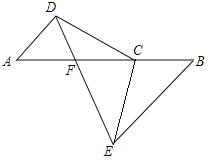
(1)求证:CD=CE;
(2)连接DE,交AB于点F,猜想△BEF的形状,并给予证明.
【答案】(1)见解析;(2)△BEF为等腰三角形,证明见解析.
【解析】
(1)先由AD∥BE得出∠A=∠B,再利用SAS证明△ADC≌△BCE即得结论;
(2)由(1)可得CD=CE,∠ACD=∠BEC,再利用等腰三角形的性质和三角形的外角性质可得∠BFE=∠BEF,进一步即得结论.
(1)证明:∵AD∥BE,∴∠A=∠B,
在△ADC和△BCE中
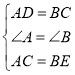
∴△ADC≌△BCE(SAS),
∴CD=CE;
(2)解:△BEF为等腰三角形,证明如下:
由(1)知△ADC≌△BCE,
∴CD=CE,∠ACD=∠BEC,
∴∠CDE=∠CED,
∴∠CDE+∠ACD=∠CED+∠BEC,
即∠BFE=∠BEF,
∴BE=BF,
∴△BEF是等腰三角形.


科目:初中数学 来源: 题型:
【题目】某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:获利=售价-进价)

(1)若商店计划销售完这批商品后能获利1 100元,请问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并指出获利最大的购货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=(2m+1)x+m﹣3
(1)若函数图象经过原点,求m的值;
(2)若函数图象与y轴的交点坐标为(0,﹣2),求m的值;
(3)若y随着x的增大而增大,求m的取值范图;
(4)若函数图象经过第一、三,四象限,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M为等腰△ABD的底AB的中点,过D作DC∥AB,连结BC;AB=8cm,DM=4cm,DC=1cm,动点P自A点出发,在AB上匀速运动,动点Q自点B出发,在折线BC﹣CD上匀速运动,速度均为1cm/s,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(s)时,△MPQ的面积为S(不能构成△MPQ的动点除外).
(1)t(s)为何值时,点Q在BC上运动,t(s)为何值时,点Q在CD上运动;
(2)求S与t之间的函数关系式;
(3)当t为何值时,S有最大值,最大值是多少?
(4)当点Q在CD上运动时,直接写出t为何值时,△MPQ是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举办“网络安全知识答题竞赛”,七、八年级根据初赛成绩各选出5名选手组成代表队参加决赛,两个队各选出的5名选手的决赛成绩如图所示.
平均分(分) | 中位数(分) | 众数(分) | 方差(分2) | |
七年级 | a | 85 | b | S七年级2 |
八年级 | 85 | c | 100 | 160 |
(1)根据图示填空:a= ,b= ,c= ;
(2)结合两队成绩的平均数和中位数进行分析,哪个代表队的决赛成绩较好?
(3)计算七年级代表队决赛成绩的方差S七年级2,并判断哪一个代表队选手成绩较为稳定.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC各顶点的坐标分别是A(﹣2,﹣4),B(0,﹣4),C(1,﹣1).
(1)在图中画出△ABC关于原点对称的△A1B1C1;
(2)在图中画出△ABC绕原点O逆时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,求点A运动路径长.
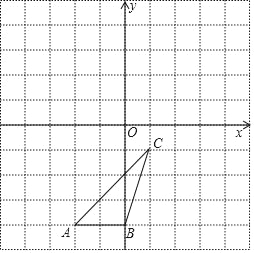
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,是两种长方形铝合金窗框,已知窗框的长都是y米,窗框的宽都是x米,若一用户需(1)型的窗框2个,(2)型的窗框2个.
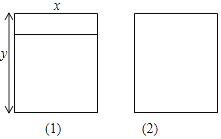
(1)用含x、y的式子表示共需铝合金的长度;
(2)若1m铝合金的平均费用为100元,求当x=1.2,y=1.5时,铝合金的总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
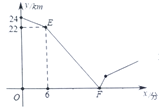
【题目】甲、乙两人在笔直的道路![]() 上相向而行,甲骑自行车从
上相向而行,甲骑自行车从![]() 地到
地到![]() 地,乙驾车从
地,乙驾车从![]() 地到
地到![]() 地,假设他们分别以不同的速度匀速行驶,甲先出6分钟后,乙才出发,乙的速度为
地,假设他们分别以不同的速度匀速行驶,甲先出6分钟后,乙才出发,乙的速度为![]() 千米/分,在整个过程中,甲、乙两人之间的距离
千米/分,在整个过程中,甲、乙两人之间的距离![]() (千米)与甲出发的时间
(千米)与甲出发的时间![]() (分)之间的部分函数图象如图.
(分)之间的部分函数图象如图.
(1)![]() 两地相距______千米,甲的速度为______千米/分;
两地相距______千米,甲的速度为______千米/分;
(2)直接写出点![]() 的坐标______,求线段
的坐标______,求线段![]() 所表示的
所表示的![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(3)当乙到达终点![]() 时,甲还需______分钟到达终点
时,甲还需______分钟到达终点![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com