
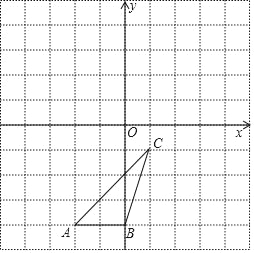
【题目】如图,△ABC各顶点的坐标分别是A(﹣2,﹣4),B(0,﹣4),C(1,﹣1).
(1)在图中画出△ABC关于原点对称的△A1B1C1;
(2)在图中画出△ABC绕原点O逆时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,求点A运动路径长.
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD是平行四边形,P是CD上的一点,且AP和BP分别分别平分∠DAB和∠CBA,QP∥AD,交AB于点Q.
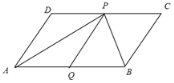
(1)求证:AP⊥PB;
(2)如果AD=5cm,AP=8cm,那么□ ABCD 的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场欲招聘一名员工,现有甲、乙两人竞聘.通过计算机、语言和商品知识三项测试,他们各自成绩(百分制)如下表所示:
应试者 | 计算机 | 语言 | 商品知识 |
甲 | 70 | 50 | 80 |
乙 | 60 | 60 | 80 |
(1)若商场需要招聘负责将商品拆装上架的人员,对计算机、语言和商品知识分别赋权2,3,5,计算两名应试者的平均成绩.从成绩看,应该录取谁?
(2)若商场需要招聘电脑收银员,计算机、语言和商品知识成绩分别占50%,30%,20%,计算两名应试者的平均成绩.从成绩看,应该录取谁?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,C是AB上一点,点D,E分别在AB两侧,AD∥BE,且AD=BC,BE=AC.
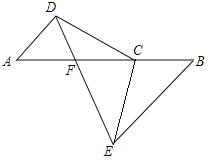
(1)求证:CD=CE;
(2)连接DE,交AB于点F,猜想△BEF的形状,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
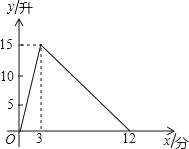
【题目】一个有进水管与出水管的容器,从某时刻开始的3分内只进水不出水,在随后的9分内既进水又出水,每分的进水量和出水量都是常数.容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图所示.
①当0≤x≤3时,求y与x之间的函数关系.
②3<x≤12时,求y与x之间的函数关系.
③当容器内的水量大于5升时,求时间x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B的中心对称得C2,C2与x轴交于另一点C,将C2关于点C的中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为_____.

【答案】32
【解析】试题分析:∵抛物线y=﹣x2﹣2x+3与x轴交于点A、B,
∴当y=0时,则﹣x2﹣2x+3=0,
解得x=﹣3或x=1,
则A,B的坐标分别为(﹣3,0),(1,0),
AB的长度为4,
从C1,C3两个部分顶点分别向下作垂线交x轴于E、F两点.
根据中心对称的性质,x轴下方部分可以沿对称轴平均分成两部分补到C1与C2.
如图所示,阴影部分转化为矩形.
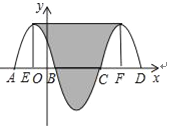
根据对称性,可得BE=CF=4÷2=2,则EF=8
利用配方法可得y=﹣x2﹣2x﹣3=﹣(x+1)2+4
则顶点坐标为(﹣1,4),即阴影部分的高为4,
S阴=8×4=32.
考点:抛物线与x轴的交点.
【题型】填空题
【结束】
17
【题目】解方程:(1)2(3x﹣1)=16;(2)![]() ;(3)
;(3)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.请你观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3…每个正方形四条边上的整点的个数.按此规律推算出正方形A10B10C10D10四条边上的整点共有______个.
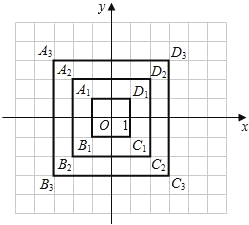
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图a是一个三角形,分别连接这个三角形三边的中点得到图b;再分别连接图b中间小三角形的三边的中点,得到图c
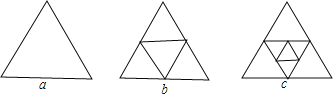
(1)图b有 个三角形,图c有 个三角形.
(2)按上面的方法继续下去,第n个图形中有多少个三角形(用n的代数式表示结论).
(3)当n=10时,第10个图形中有多少个三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知坐标平面内的三个点![]() ,
,![]() ,
,![]() ,把
,把![]() 向下平移
向下平移![]() 个单位再向右平移
个单位再向右平移![]() 个单位后得
个单位后得![]() .
.

(1)画出平移后的图形,直接写出![]() ,
,![]() ,
,![]() 三个对应点
三个对应点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(2)求![]() 的面积。
的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com