
【题目】已知:如图,四边形ABCD是平行四边形,P是CD上的一点,且AP和BP分别分别平分∠DAB和∠CBA,QP∥AD,交AB于点Q.
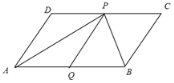
(1)求证:AP⊥PB;
(2)如果AD=5cm,AP=8cm,那么□ ABCD 的面积是多少?
【答案】(1)见解析;(2)48 cm2.
【解析】
(1)根据平行四边形性质得出AD∥CB,AB∥CD,推出∠DAB+∠CBA=180°,求出∠PAB+∠PBA=90°,在△APB中求出∠APB即可;
(2)根据平行四边形性质得出AD∥CB,AB∥CD,由已知QP∥AD可证四边形DAQP、PQBC是平行四边形,则![]() ,
,![]() ,即□ ABCD 的面积=2
,即□ ABCD 的面积=2![]() ,求出AD=DP=5,BC=PC=5,求出DC=10=AB,由勾股定理求出BP,求出
,求出AD=DP=5,BC=PC=5,求出DC=10=AB,由勾股定理求出BP,求出![]() ,即可求出答案.
,即可求出答案.
证明:(1)∵ABCD是平行四边形,
∴AD∥CB.∴∠DAB+∠CBA=180°.
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA=![]() (∠DAB+∠CBA)=90°.
(∠DAB+∠CBA)=90°.
在△APB中,∵∠APB=180°-(∠PAB+∠PBA)=90°.
∴AP⊥PB;
(2)∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∵QP∥AD
∴四边形DAQP、PQBC是平行四边形,
∴![]() ,
,![]() ,
,
∴□ ABCD 的面积=2![]() ,
,
∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD,
∴∠PAB=∠DPA
∴∠DAP=∠DPA
∴△ADP是等腰三角形,
∴AD=DP=5,
同理:PC=CB=5,
即AB=DC=DP+PC=10,
在Rt△APB中,AB=10,AP=8,
∴BP=![]() =6,
=6,
∴△ABP的面积为:![]() ×6×8=24(cm2)
×6×8=24(cm2)
∴□ ABCD 的面积=2![]() =48 cm2.
=48 cm2.
故答案为:(1)见解析;(2)48 cm2.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
【题目】已知![]() 为有理数,定义一种新运算,其意义是
为有理数,定义一种新运算,其意义是![]()
![]() ,试根据这种运算完成下列各题
,试根据这种运算完成下列各题
(1)求①23;②(43)(-2)
(2)任意选择两个有理数,分别代替![]() 与
与![]() ,并比较
,并比较![]() 和
和![]() 两个运算的结果,你有何发现;
两个运算的结果,你有何发现;
(3)根据以上方法,探索![]() 的关系,并用等式把它们表示出来.
的关系,并用等式把它们表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
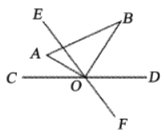
【题目】如图,直线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,将一直角三角尺
,将一直角三角尺![]() 的直角顶点与点
的直角顶点与点![]() 重合,
重合,![]() 平分
平分![]() .
.
(1)![]() 的度数为______________
的度数为______________![]() ;
;
(2)将三角尺![]() 以每秒
以每秒![]() 的速度绕点
的速度绕点![]() 顺时针旋转,同时直线
顺时针旋转,同时直线![]() 也以每秒
也以每秒![]() 的速度绕点
的速度绕点![]() 顺时针旋转,设运动时间为
顺时针旋转,设运动时间为![]() 秒
秒![]() .
.
①求当![]() 为何值时,直线
为何值时,直线![]() 平分
平分![]() ;
;
②求当![]() 为何值时,直线
为何值时,直线![]() 平分
平分![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
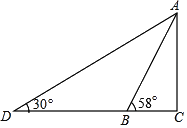
【题目】如图,某游乐园有一个滑梯高度AB,高度AC为3米,倾斜角度为58°.为了改善滑梯AB的安全性能,把倾斜角由58°减至30°,调整后的滑梯AD比原滑梯AB增加多少米?(精确到0.1米)
(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a+b+c<0;②a-b+c<0;③b+2a<0;④abc>0,其中正确的是( )
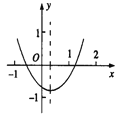
A. ①②③ B. ②③ C. ③④ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:获利=售价-进价)

(1)若商店计划销售完这批商品后能获利1 100元,请问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并指出获利最大的购货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
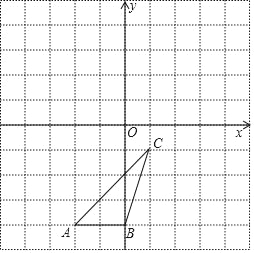
【题目】如图,△ABC各顶点的坐标分别是A(﹣2,﹣4),B(0,﹣4),C(1,﹣1).
(1)在图中画出△ABC关于原点对称的△A1B1C1;
(2)在图中画出△ABC绕原点O逆时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,求点A运动路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com