
【题目】如图1,抛物线y=ax2﹣6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在x轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
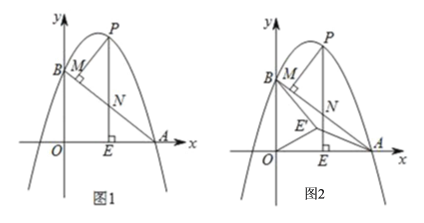
(1)求出抛物线的函数表达式;
(2)设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;
(3)如图2,在(2)条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为30°,连接E'A、E'B,在坐标平面内找一点Q,使△AOE′~△BOQ,并求出Q的坐标.
【答案】(1)y=-![]() x2+
x2+![]() x+6;(2)m=4;(3)Q1(
x+6;(2)m=4;(3)Q1(![]() ,
,![]() ),Q2(﹣
),Q2(﹣![]() ,
,![]() ).
).
【解析】
(1)把点A(8,0)代入抛物线解析式求解即得;
(2)易求得直线AB解析式为y=![]() x+6,再证明△ANE∽△PNM,由相似三角形的性质得
x+6,再证明△ANE∽△PNM,由相似三角形的性质得![]() ,由E(m,0)(0<m<8)可得P(m,
,由E(m,0)(0<m<8)可得P(m,![]() ),N(m,
),N(m,![]() m+6),然后用m的代数式表示出AN和PN,解方程即可;
m+6),然后用m的代数式表示出AN和PN,解方程即可;
(3)由题意可求得OQ的长,过点Q作QH⊥y轴于H,然后利用∠BOQ=∠AOE′=30°,可求得QH和OH的长,进一步即得结果.
解:(1)把A(8,0)代入y=ax2﹣6ax+6,得64a﹣48a+6=0,解得a=![]() ,
,
∴抛物线的函数表达式为:y=![]() x2+
x2+![]() x+6;
x+6;
(2)如图1,在y=![]() x2+
x2+![]() x+6中,令x=0,得y=6,∴B(0,6),
x+6中,令x=0,得y=6,∴B(0,6),
设直线AB解析式为y=kx+b,则![]() ,解得
,解得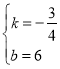 ,
,
∴直线AB解析式为y=![]() x+6
x+6
∵PE⊥x轴,PM⊥AB
∴∠AEN=∠PMN=90°,
∵∠ANE=∠PNM,∴△ANE∽△PNM.
∴![]() ,
,![]() ,
,
∵S1:S2=36:25,

∴![]() ,
,
∴6AN=5PN
∵E(m,0)(0<m<8),∴OE=m,AE=8﹣m,
∴P(m,![]() ),N(m,
),N(m,![]() m+6),
m+6),
∴EN=![]() m+6,PN=PE﹣EN=
m+6,PN=PE﹣EN=![]() ﹣(
﹣(![]() m+6)=
m+6)=![]() +3m,
+3m,
∵AB=![]() =10
=10
∴cos∠OAB=![]() ,即
,即![]() ,
,
∴AN=![]() (8﹣m),
(8﹣m),
∴6×![]() (8﹣m)=5×(
(8﹣m)=5×(![]() +3m),解得:m1=4,m2=8(不符合题意,舍去),
+3m),解得:m1=4,m2=8(不符合题意,舍去),
∴m=4;
(3)如图2,∵线段OE绕点O逆时针旋转得到OE′,旋转角为30°,
∴OE′=OE=4,∠AOE′=30°
∵△AOE′∽△BOQ,
∴![]() ,∠BOQ=∠AOE′=30°,
,∠BOQ=∠AOE′=30°,
∴![]() ,即OQ=3,
,即OQ=3,
过点Q作QH⊥y轴于H,
∴QH=![]() OQ=
OQ=![]() ,OH=
,OH=![]() ,
,
∴当点Q在y轴右侧时,Q1(![]() ,
,![]() ),
),
当点Q在y轴左侧时,Q2(﹣![]() ,
,![]() ).
).
综上所述,Q的坐标为:Q1(![]() ,
,![]() ),Q2(﹣
),Q2(﹣![]() ,
,![]() ).
).


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
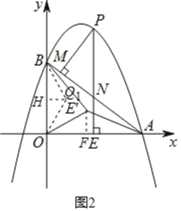
【题目】如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于E,CG是⊙F的切线,CG交AD于点G.
(1)求证:CG⊥AD;
(2)填空:
①若△BDA的面积为80,则△BCF的面积为 ;
②当∠BAD的度数为 时,四边形EFCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.

(1)求二次函数解析式;
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形![]() .是否存在点P,使四边形
.是否存在点P,使四边形![]() 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
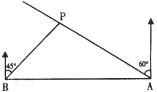
【题目】如图,在一笔直的海岸线上有A,B两个观测站,A在B的正东方向,有一艘小船停在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,BP=6![]() km.
km.
(1)求A、B两观测站之间的距离;
(2)小船从点P处沿射线AP的方向前行,求观测站B与小船的最短距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
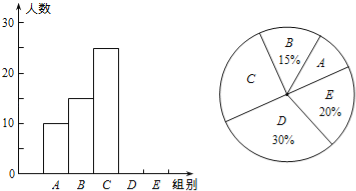
【题目】某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息解决下列问题:
(1)在统计表中,m= ,n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)若该校共有900名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
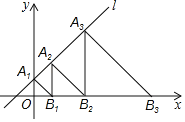
【题目】如图,在平面直角坐标系xOy中,直线l:y=x+1交y轴于点A1,点A2,A3,…,An在直线l上,点B1,B2,B3,…,Bn在x轴的正半轴上,若△OA1B1,△A2B1B2,△A3B2B3,…,△AnBn﹣1Bn依次均为等腰直角三角形,则点B1的坐标是_____;点Bn的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
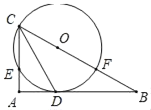
【题目】如图,Rt△ABC中,∠A=90°,CD平分∠ACB交AB于点D,O是BC上一点,经过C、D两点的⊙O分别交AC、BC于点E、F,AD=![]() ,∠ADC=60°,则劣弧
,∠ADC=60°,则劣弧![]() 的长为_____.
的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》、《大学》、《中庸》(依次用字母A,B,C表示这三个材料),将A,B,C分别写在3张完全相同的不透明卡片的正面上,背面朝上洗匀后放在桌面上,比赛时小礼先从中随机抽取一张卡片,记下内容后放回,洗匀后,再由小智从中随机抽取一张卡片,他俩按各自抽取的内容进行诵读比赛.
(1)小礼诵读《论语》的概率是 ;(直接写出答案)
(2)请用列表或画树状图的方法求他俩诵读两个不同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都为1,每个小正方形的顶点叫格点.请完成如图所示的画图,要求:①仅用无刻度的直尺,②不写画法,保留必要的画图痕迹.
(1)在图1中画出一条长为![]() 的线段MN(M,N分别为格点)
的线段MN(M,N分别为格点)
(2)在图2中画出一个以格点为顶点,以AB为一边的正方形ABCD;
(3)在图3中,E,F分别为格点,画出线段EF的垂直平分线l.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com