
ЁОЬтФПЁПЦћГЕЕФЁАШМгЭаЇТЪЁБЪЧжИЦћГЕУПЯћКФ1Щ§ЦћгЭааЪЛЕФзюДѓЙЋРяЪ§ЃЈЕЅЮЛЃК![]() ЃЉЃЌШчЭМУшЪіСЫМзЁЂввЁЂБћШ§СОЦћГЕдкВЛЭЌЫйЖШЯТЕФШМгЭаЇТЪЧщПіЃЌЯТСаа№Ъіе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
ЃЉЃЌШчЭМУшЪіСЫМзЁЂввЁЂБћШ§СОЦћГЕдкВЛЭЌЫйЖШЯТЕФШМгЭаЇТЪЧщПіЃЌЯТСаа№Ъіе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
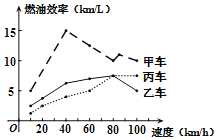
A.ЕБааЪЛЫйЖШЮЊ![]() ЪБЃЌУПЯћКФ1Щ§ЦћгЭЃЌМзГЕФмааЪЛ
ЪБЃЌУПЯћКФ1Щ§ЦћгЭЃЌМзГЕФмааЪЛ![]()
B.ЯћКФ1Щ§ЦћгЭЃЌБћГЕзюЖрПЩааЪЛ![]()
C.ЕБааЪЛЫйЖШЮЊ![]() ЪБЃЌУПЯћКФ1Щ§ЦћгЭЃЌввГЕКЭБћГЕааЪЛЕФзюДѓЙЋРяЪ§ЯрЭЌ
ЪБЃЌУПЯћКФ1Щ§ЦћгЭЃЌввГЕКЭБћГЕааЪЛЕФзюДѓЙЋРяЪ§ЯрЭЌ
D.ЕБааЪЛЫйЖШЮЊ![]() ЪБЃЌШєааЪЛЯрЭЌЕФТЗГЬЃЌБћГЕЯћКФЕФЦћгЭзюЩй
ЪБЃЌШєааЪЛЯрЭЌЕФТЗГЬЃЌБћГЕЯћКФЕФЦћгЭзюЩй
ЁОД№АИЁПC
ЁОНтЮіЁП
ИљОнКЏЪ§ЭМЯѓЕУГіаЁЪЏЦяааФІАнЕЅГЕЕФТЗГЬЮЊЃК![]() ЃЌааЪЛЕФЫйЖШЮЊЃКЃЈ1Љ0.6ЃЉаЁЪБЃЌНјЖјЧѓГіЫйЖШМДПЩЃЎ
ЃЌааЪЛЕФЫйЖШЮЊЃКЃЈ1Љ0.6ЃЉаЁЪБЃЌНјЖјЧѓГіЫйЖШМДПЩЃЎ
AЁЂЕБааЪЛЫйЖШЮЊ![]() ЪБЃЌУПЯћКФ1Щ§ЦћгЭЃЌМзГЕФмааЪЛ
ЪБЃЌУПЯћКФ1Щ§ЦћгЭЃЌМзГЕФмааЪЛ![]() ЃЌДэЮѓЃЛ
ЃЌДэЮѓЃЛ
BЁЂЯћКФ1Щ§ЦћгЭЃЌБћГЕзюЖрПЩааЪЛДѓгк![]() ЃЌДэЮѓЃЛ
ЃЌДэЮѓЃЛ
CЁЂЕБааЪЛЫйЖШЮЊ![]() ЪБЃЌУПЯћКФ1Щ§ЦћгЭЃЌввГЕКЭБћГЕааЪЛЕФзюДѓЙЋРяЪ§ЯрЭЌЃЌе§ШЗЃЛ
ЪБЃЌУПЯћКФ1Щ§ЦћгЭЃЌввГЕКЭБћГЕааЪЛЕФзюДѓЙЋРяЪ§ЯрЭЌЃЌе§ШЗЃЛ
DЁЂЕБааЪЛЫйЖШЮЊ![]() ЪБЃЌШєааЪЛЯрЭЌЕФТЗГЬЃЌМзГЕЯћКФЕФЦћгЭзюЩйЃЌДэЮѓЃЛ
ЪБЃЌШєааЪЛЯрЭЌЕФТЗГЬЃЌМзГЕЯћКФЕФЦћгЭзюЩйЃЌДэЮѓЃЛ
ЙЪбЁЃКCЃЎ


 ЕМбЇНЬГЬИпжааТПЮБъЯЕСаД№АИ
ЕМбЇНЬГЬИпжааТПЮБъЯЕСаД№АИ аЁбЇПЮЪБЬибЕЯЕСаД№АИ
аЁбЇПЮЪБЬибЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
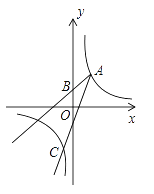
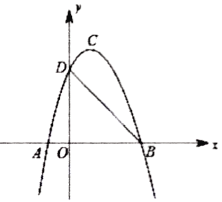
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуA(2,3)КЭЕуB(0,2)ЃЌЕуAдкЗДБШР§КЏЪ§y= ![]() ЕФЭМЯѓЩЯ.зїЩфЯпABЃЌдйНЋЩфЯпABШЦЕуAАДФцЪБеыЗНЯђа§зЊ45ЁуЃЌНЛЗДБШР§КЏЪ§ЭМЯѓгкЕуCЃЌдђЕуCЕФзјБъЮЊ________.
ЕФЭМЯѓЩЯ.зїЩфЯпABЃЌдйНЋЩфЯпABШЦЕуAАДФцЪБеыЗНЯђа§зЊ45ЁуЃЌНЛЗДБШР§КЏЪ§ЭМЯѓгкЕуCЃЌдђЕуCЕФзјБъЮЊ________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОдкПЙе№ОШджЦкМфГаЕЃ40 000ЖЅОШджеЪХёЕФЩњВњШЮЮёЃЌЗжЮЊAЁЂBЁЂCЁЂDЫФжжаЭКХЃЌЫќУЧЕФЪ§СПАйЗжБШКЭУПЬьЕЅЖРЩњВњИїжжаЭКХеЪХёЕФЪ§СПШчЭМЫљЪОЃК

ИљОнвдЩЯаХЯЂЃЌЯТСаХаЖЯДэЮѓЕФЪЧЃЈ ЃЉ
A. ЦфжаЕФDаЭеЪХёеМеЪХёзмЪ§ЕФ10%
B. ЕЅЖРЩњВњBаЭеЪХёЕФЬьЪ§ЪЧЕЅЖРЩњВњCаЭеЪХёЬьЪ§ЕФ3БЖ
C. ЕЅЖРЩњВњAаЭеЪХёгыЕЅЖРЩњВњDаЭеЪХёЕФЬьЪ§ЯрЕШ
D. ЕЅЖРЩњВњBаЭеЪХёЕФЬьЪ§ЪЧЕЅЖРЩњВњAаЭеЪХёЬьЪ§ЕФ2БЖ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌACЃНBCЃЌЕуDЪЧACбгГЄЯпЩЯвЛЕуЃЌСЌНсBDЃЎНЋ
ЃЌACЃНBCЃЌЕуDЪЧACбгГЄЯпЩЯвЛЕуЃЌСЌНсBDЃЎНЋ![]() ШЦзХЕуCЫГЪБеыа§зЊ90ЁуЕУЕН
ШЦзХЕуCЫГЪБеыа§зЊ90ЁуЕУЕН![]() ЃЌбгГЄAEНЛBDгкFЃЎ
ЃЌбгГЄAEНЛBDгкFЃЎ
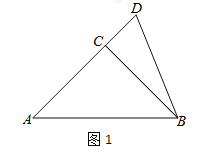
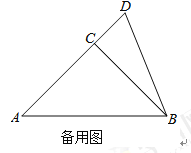
ЃЈ1ЃЉвРОнЬтвтВЙШЋЭМ1ЃЛ
ЃЈ2ЃЉХаЖЯAEгыBDЕФЮЛжУЙиЯЕЃЌЫЕУїРэгЩЃЛ
ЃЈ3ЃЉСЌНсCFЃЌЧѓ![]() ЕФЖШЪ§ЃЎ
ЕФЖШЪ§ЃЎ
вЊЯыЧѓГі![]() ЕФЖШЪ§ЃЌаЁУїОЙ§ЫМПМЃЌЕУЕНСЫвдЯТМИжжЯыЗЈЃК
ЕФЖШЪ§ЃЌаЁУїОЙ§ЫМПМЃЌЕУЕНСЫвдЯТМИжжЯыЗЈЃК
ЯыЗЈ1ЃКдкAFЩЯШЁвЛЕуGЃЌЪЙЕУAGЃНBFЃЌашвЊЯШжЄУї![]() ЃЌШЛКѓдйжЄУї
ЃЌШЛКѓдйжЄУї![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЎ
ЪЧЕШбќжБНЧШ§НЧаЮЃЎ
ЯыЗЈ2ЃКШЁABЕФжаЕуOЃЌСЌНгOCЃЌOFЃЌжЛашвЊРћгУдВЕФаджЪжЄУї![]() ЃЎ
ЃЎ
ЯыЗЈ3ЃКНЋ![]() ШЦЕуCФцЪБеыа§зЊ90ЁуЃЌЕУЕН
ШЦЕуCФцЪБеыа§зЊ90ЁуЃЌЕУЕН![]() ЃЌжЛашжЄУї
ЃЌжЛашжЄУї![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЎ
ЪЧЕШбќжБНЧШ§НЧаЮЃЎ
ЧыФуВЮПМЩЯУцЕФЯыЗЈЃЌАяжњаЁУїЧѓНтЃЎЃЈаДГівЛжжЗНЗЈМДПЩЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
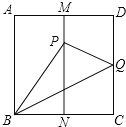
ЁОЬтФПЁПШчЭМЃЌвбжЊе§ЗНаЮжНЦЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЁЂ
ЁЂ![]() ЗжБ№ЪЧБп
ЗжБ№ЪЧБп![]() ЁЂ
ЁЂ![]() ЕФжаЕуЃЌАб
ЕФжаЕуЃЌАб![]() БпЯђЩЯЗелЃЌЪЙЕу
БпЯђЩЯЗелЃЌЪЙЕу![]() ЧЁКУТфдк
ЧЁКУТфдк![]() ЩЯЕФ
ЩЯЕФ![]() ЕуДІЃЌ
ЕуДІЃЌ![]() ЮЊелКлЃЌЧв
ЮЊелКлЃЌЧв![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌдђ
ЃЌдђ![]() ЕФУцЛ§ЮЊ_____ЃЎ
ЕФУцЛ§ЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЖдЁАИєРыжБЯпЁБИјГіШчЯТЖЈвхЃК
ЕуPЃЈxЃЌmЃЉЪЧЭМаЮG1ЩЯЕФШЮвтвЛЕуЃЌЕуQЃЈxЃЌnЃЉЪЧЭМаЮG2ЩЯЕФШЮвтвЛЕуЃЌШєДцдкжБЯпlЃКkx+bЃЈkЁй0ЃЉТњзуmЁмkx+bЧвnЁнkx+bЃЌдђГЦжБЯпlЃКy=kx+bЃЈkЁй0ЃЉЪЧЭМаЮG1гыG2ЕФЁАИєРыжБЯпЁБЃЎ
ШчЭМЃЌжБЯпlЃКy=-x-4ЪЧКЏЪ§y=![]() ЃЈxЃМ0ЃЉЕФЭМЯѓгые§ЗНаЮOABCЕФвЛЬѕЁАИєРыжБЯпЁБЃЎ
ЃЈxЃМ0ЃЉЕФЭМЯѓгые§ЗНаЮOABCЕФвЛЬѕЁАИєРыжБЯпЁБЃЎ
ЃЈ1ЃЉдкжБЯпy1=-2xЃЌy2=3x+1ЃЌy3=-x+3жаЃЌЪЧШчЭМКЏЪ§y=![]() ЃЈxЃМ0ЃЉЕФЭМЯѓгые§ЗНаЮOABCЕФЁАИєРыжБЯпЁБЕФЮЊy1=-2xЃЛ
ЃЈxЃМ0ЃЉЕФЭМЯѓгые§ЗНаЮOABCЕФЁАИєРыжБЯпЁБЕФЮЊy1=-2xЃЛ
ЧыФудйаДГівЛЬѕЗћКЯЬтвтЕФВЛЭЌЕФЁАИєРыжБЯпЁБЕФБэДяЪНЃКy=-3xЃЛ
ЃЈ2ЃЉШчЭМЃЌЕквЛЯѓЯоЕФЕШбќжБНЧШ§НЧаЮEDFЕФСНбќЗжБ№гызјБъжсЦНааЃЌжБНЧЖЅЕуDЕФзјБъЪЧЃЈ![]() ЃЌ1ЃЉЃЌЁбOЕФАыОЖЮЊ2ЃЎЪЧЗёДцдкЁїEDFгыЁбOЕФЁАИєРыжБЯпЁБЃПШєДцдкЃЌЧѓГіДЫЁАИєРыжБЯпЁБЕФБэДяЪНЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЌ1ЃЉЃЌЁбOЕФАыОЖЮЊ2ЃЎЪЧЗёДцдкЁїEDFгыЁбOЕФЁАИєРыжБЯпЁБЃПШєДцдкЃЌЧѓГіДЫЁАИєРыжБЯпЁБЕФБэДяЪНЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉе§ЗНаЮA1B1C1D1ЕФвЛБпдкyжсЩЯЃЌЦфЫќШ§БпЖМдкyжсЕФгвВрЃЌЕуMЃЈ1ЃЌtЃЉЪЧДЫе§ЗНаЮЕФжааФЃЎШєДцдкжБЯпy=2x+bЪЧКЏЪ§y=x2-2x-3ЃЈ0ЁмxЁм4ЃЉЕФЭМЯѓгые§ЗНаЮA1B1C1D1ЕФЁАИєРыжБЯпЁБЃЌЧыжБНгаДГіtЕФШЁжЕЗЖЮЇЃЎ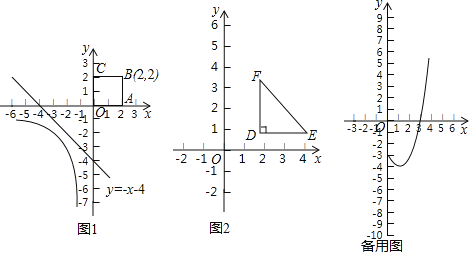
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌAB=BCЃЌЁЯABC=90ЁуЃЎвдABЮЊаББпзїЕШбќжБНЧШ§НЧаЮADBЃЎЕуPЪЧжБЯпDBЩЯвЛИіЖЏЕуЃЌСЌНгAPЃЌзїPEЁЭAPНЛBCЫљдкЕФжБЯпгкЕуEЃЎ

ЃЈ1ЃЉШчЭМ1ЃЌЕуPдкBDЕФбгГЄЯпЩЯЃЌPEЁЭECЃЌAD=1ЃЌжБНгаДГіPEЕФГЄЃЛ
ЃЈ2ЃЉЕуPдкЯпЖЮBDЩЯЃЈВЛгыBЃЌDжиКЯЃЉЃЌвРЬтвтЃЌНЋЭМ2ВЙШЋЃЌЧѓжЄЃКPA=PEЃЛ
ЃЈ3ЃЉЕуPдкDBЕФбгГЄЯпЩЯЃЌвРЬтвтЃЌНЋЭМ3ВЙШЋЃЌВЂХаЖЯPA=PEЪЧЗёШдШЛГЩСЂЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
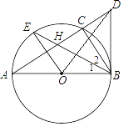
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌCЪЧЁбOЪЧвЛЕуЃЌЙ§ЕуBзїЁбOЕФЧаЯпЃЌгыACбгГЄЯпНЛгкЕуDЃЌСЌНгBCЃЌOE//BCНЛЁбOгкЕуEЃЌСЌНгBEНЛACгкЕуHЁЃЃЈ1ЃЉЧѓжЄЃКBEЦНЗжЁЯABCЃЛЃЈ2ЃЉСЌНгODЃЌШєBH=BD=2ЃЌЧѓODЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§![]() ЕФЭМЯѓНЛ
ЕФЭМЯѓНЛ![]() жсгк
жсгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌНЛ
СНЕуЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЖЅЕу
ЃЌЖЅЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() .
.
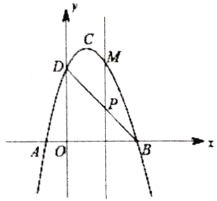
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФБэДяЪНКЭжБЯп![]() ЕФБэДяЪНЃЛ
ЕФБэДяЪНЃЛ
ЃЈ2ЃЉЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯЕФвЛИіЖЏЕуЃЌЙ§Еу
ЩЯЕФвЛИіЖЏЕуЃЌЙ§Еу![]() зї
зї![]() жсЕФДЙЯпЃЌНЛХзЮяЯпгкЕу
жсЕФДЙЯпЃЌНЛХзЮяЯпгкЕу![]() ЃЌЕБЕу
ЃЌЕБЕу![]() дкЕквЛЯѓЯоЪБЃЌЧѓЯпЖЮ
дкЕквЛЯѓЯоЪБЃЌЧѓЯпЖЮ![]() ГЄЖШЕФзюДѓжЕЃЛ
ГЄЖШЕФзюДѓжЕЃЛ
ЃЈ3ЃЉдкХзЮяЯпЩЯДцдквьгк![]() ЁЂ
ЁЂ![]() ЕФЕу
ЕФЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() жа
жа![]() БпЩЯЕФИпЮЊ
БпЩЯЕФИпЮЊ![]() ЃЌЧыжБНгаДГіЕу
ЃЌЧыжБНгаДГіЕу![]() ЕФзјБъ.
ЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com