
【题目】如图,在![]() 中,
中,![]() ,AC=BC,点D是AC延长线上一点,连结BD.将
,AC=BC,点D是AC延长线上一点,连结BD.将![]() 绕着点C顺时针旋转90°得到
绕着点C顺时针旋转90°得到![]() ,延长AE交BD于F.
,延长AE交BD于F.
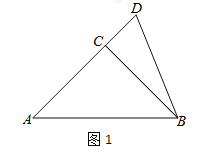
(1)依据题意补全图1;
(2)判断AE与BD的位置关系,说明理由;
(3)连结CF,求![]() 的度数.
的度数.
要想求出![]() 的度数,小明经过思考,得到了以下几种想法:
的度数,小明经过思考,得到了以下几种想法:
想法1:在AF上取一点G,使得AG=BF,需要先证明![]() ,然后再证明
,然后再证明![]() 是等腰直角三角形.
是等腰直角三角形.
想法2:取AB的中点O,连接OC,OF,只需要利用圆的性质证明![]() .
.
想法3:将![]() 绕点C逆时针旋转90°,得到
绕点C逆时针旋转90°,得到![]() ,只需证明
,只需证明![]() 是等腰直角三角形.
是等腰直角三角形.
请你参考上面的想法,帮助小明求解.(写出一种方法即可)
【答案】(1)详见解析;(2)详见解析;(3)详见解析.
【解析】
(1)根据题意补全图形即可;
(2)利用旋转的性质得出![]() ,再利用同角的余角相等即可得出结论;
,再利用同角的余角相等即可得出结论;
(3)想法1、利用SAS判断出![]() 即可得出结论;想法2、利用
即可得出结论;想法2、利用![]() 即可判断出点A,B,F,C四点在以O为圆心OA为半径的圆上即可得出结论;想法3,利用旋转的性质判断出
即可判断出点A,B,F,C四点在以O为圆心OA为半径的圆上即可得出结论;想法3,利用旋转的性质判断出![]() 是等腰直角三角形即可得出结论.
是等腰直角三角形即可得出结论.
(1)补全图形如图1所示.
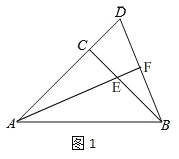
(2)∵将![]() 绕着点C顺时针旋转90°得到
绕着点C顺时针旋转90°得到![]()
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
(3)想法1、如图2, 在AF上取一点G,使得![]() ,连接CG.
,连接CG.
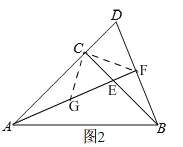
![]() ,
,![]() ,
,![]() ,
,
![]() .
.
![]() ,
,![]() .
.
![]() ,
,
![]() .
.
∴△CFG是等腰直角三角形.
![]() .
.
想法2、如图3,
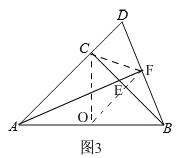
取AB的中点O,连接OC,OF,CF,
![]() 是直角三角形,
是直角三角形,
![]() ,
,
由(2)知,![]() ,
,
![]() ,
,
![]() ,
,
∴点A,B,F,C在以O为圆心,OA为半径的圆上,
![]() ,
,
想法3、如图4,
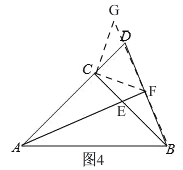
将![]() 绕点C逆时针旋转90°得到
绕点C逆时针旋转90°得到![]() ,
,
![]() ,
,![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
由(1)![]() ,
,
∴点G在BD的延长线上,
由(2)知,![]() ,
,
![]() .
.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:初中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程数.“燃油效率”越高表示汽车每消耗1升汽油行驶的里程数越多;“燃油效率”越低表示汽车每消耗1升汽油行驶的里程数越少.如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列说法中,正确的是( )
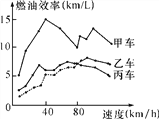
A. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
B. 以低于80 km/h的速度行驶时,行驶相同路程,三辆车中,乙车消耗汽油最少
C. 以高于80 km/h的速度行驶时,行驶相同路程,丙车比乙车省油
D. 以80 km/h的速度行驶时,行驶100公里,甲车消耗的汽油量约为10升
查看答案和解析>>
科目:初中数学 来源: 题型:
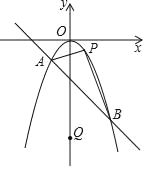
【题目】如图所示,已知抛物线y=ax2(a≠0)与一次函数y=kx+b的图象相交于A(﹣1,﹣1),B(2,﹣4)两点,点P是抛物线上不与A,B重合的一个动点,点Q是y轴上的一个动点.
(1)请直接写出a,k,b的值及关于x的不等式ax2<kx﹣2的解集;
(2)当点P在直线AB上方时,请求出△PAB面积的最大值并求出此时点P的坐标;
(3)是否存在以P,Q,A,B为顶点的四边形是平行四边形?若存在,请直接写出P,Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
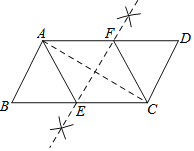
已知:如图,四边形![]() 是平行四边形.求作:菱形
是平行四边形.求作:菱形![]() ,使点
,使点![]() 分别在
分别在![]() 上.
上.
小凯的作法如下:
(1)连接![]() ;
;
(2)作![]() 的垂直平分线
的垂直平分线![]() 分别交
分别交![]() 于
于![]() ;
;
(3)连接![]() .
.
所以四边形![]() 是菱形.
是菱形.
老师说:“小凯的作法正确.”
请回答:在小凯的作法中,判定四边形![]() 是菱形的依据是__________.
是菱形的依据是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,D是BC边的中点,连接AD,过点A作AE∥BC,且AE=CD,连接EC.
,D是BC边的中点,连接AD,过点A作AE∥BC,且AE=CD,连接EC.
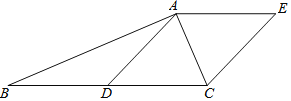
(1)求证:四边形ADCE是菱形;
(2)如果![]() ,
,![]() ,写出求菱形ADCE的面积的思路.
,写出求菱形ADCE的面积的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“美丽抚顺”的工作部署,市政府计划对城区道路进行了改造,现安排甲、乙两个工程队完成.已知甲队的工作效率是乙队工作效率的![]() 倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
(1)甲、乙两工程队每天能改造道路的长度分别是多少米?
(2)若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,如需改造的道路全长1200米,改造总费用不超过145万元,至少安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:![]() ),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( )
),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( )
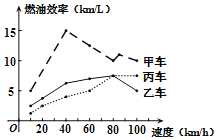
A.当行驶速度为![]() 时,每消耗1升汽油,甲车能行驶
时,每消耗1升汽油,甲车能行驶![]()
B.消耗1升汽油,丙车最多可行驶![]()
C.当行驶速度为![]() 时,每消耗1升汽油,乙车和丙车行驶的最大公里数相同
时,每消耗1升汽油,乙车和丙车行驶的最大公里数相同
D.当行驶速度为![]() 时,若行驶相同的路程,丙车消耗的汽油最少
时,若行驶相同的路程,丙车消耗的汽油最少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】顺义区某中学举行春季运动会,初二年级决定从本年级300名女生中挑选64人组成花束方队,要求身高基本一致,这个工作交给年级学生会体育部小红、小冬和小芳来完成.
为了达到年级的选拔要求,小红、小冬和小芳各自对本学校初二年级的女生身高进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1 小红抽样调查初二年级4名女同学身高统计表(单位:![]() )
)
序号 | 1 | 2 | 3 | 4 |
身高 | 155 | 160 | 165 | 172 |
表2小冬抽样调查初二年级15名女同学身高统计表(单位:![]() )
)
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
身高 | 148 | 149 | 150 | 152 | 152 | 160 | 160 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 175 |
表3小芳抽样调查初二年级15名女同学身高统计表(单位:![]() )
)
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
身高 | 145 | 160 | 150 | 152 | 160 | 154 | 160 | 166 | 167 | 168 | 160 | 169 | 173 | 174 | 175 |
根据自己的调查数据,小红说应选取身高为163![]() (数据的平均数)的同学参加方队,小冬说应选取身高为165
(数据的平均数)的同学参加方队,小冬说应选取身高为165![]() (数据的中位数)的同学参加方队,小芳说应选取身高为160
(数据的中位数)的同学参加方队,小芳说应选取身高为160![]() (数据的众数)的同学参加方队.根据以上材料回答问题:
(数据的众数)的同学参加方队.根据以上材料回答问题:
小红、小冬和小芳三人中,哪一位同学的抽样调查及得出的结论更符合年级的要求,并简要说明符合要求的理由,同时其他两位同学的抽样调查或得出结论的不足之处.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠BAC=90°,AB=2,边AB在x轴上,BC边上的中线AD的反向延长线交y轴于点E(0,3),反比例函数y=![]() (x>0)的图象过点C,则k的值为_____.
(x>0)的图象过点C,则k的值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com