Question

【题目】如图，梯形ABCD中，AD∥BC，∠ABC=2∠BCD=2α，点E在AD上，点F在DC上，且∠BEF=∠A．

（1）∠BEF=（用含α的代数式表示）；
（2）当AB=AD时，猜想线段EB、EF的数量关系，并证明你的猜想；
（3）当AB≠AD时，将“点E在AD上”改为“点E在AD的延长线上，且AE＞AB，AB=mDE，AD=nDE”，其他条件不变（如图），求 的值（用含m，n的代数式表示）

Answer 1

【答案】
（1）解：∵梯形ABCD中，AD∥BC，
∴∠A+∠ABC=180°，
∴∠A=180°﹣∠ABC=180°﹣2α，
又∵∠BEF=∠A，
∴∠BEF=∠A=180°﹣2α；
故答案为：180°﹣2α；
（2）

EB=EF．

证明：连接BD交EF于点O，连接BF．

∵AD∥BC，

∴∠A=180°﹣∠ABC=180°﹣2α，∠ADC=180°﹣∠C=180°﹣α．

∵AB=AD，

∴∠ADB= （180°﹣∠A）=α，

∴∠BDC=∠ADC﹣∠ADB=180°﹣2α，

由（1）得：∠BEF=180°﹣2α=∠BDC，

又∵∠EOB=∠DOF，

∴△EOB∽△DOF，

∴ ，

即 ，

∵∠EOD=∠BOF，

∴△EOD∽△BOF，

∴∠EFB=∠EDO=α，

∴∠EBF=180°﹣∠BEF﹣∠EFB=α=∠EFB，

∴EB=EF；

（3）

解：延长AB至G，使AG=AE，连接GE，

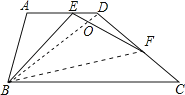
则∠G=∠AEG= = =α，

∵AD∥BC，

∴∠EDF=∠C=α，∠GBC=∠A，∠DEB=∠EBC，

∴∠EDF=∠G，

∵∠BEF=∠A，

∴∠BEF=∠GBC，

∴∠GBC+∠EBC=∠DEB+∠BEF，

即∠EBG=∠FED，

∴△DEF∽△GBE，

∴ ，

∵AB=mDE，AD=nDE，

∴AG=AE=（n+1）DE，

∴BG=AG﹣AB=（n+1）DE﹣mDE=（n+1﹣m）DE，

∴ = =n+1﹣m．

【解析】【分 析】（1）由梯形ABCD中，AD∥BC，∠ABC=2∠BCD=2α，根据平行线的性质，易求得∠A的度数，又由∠BEF=∠A，即可求得∠BEF的度 数；（2）首先连接BD交EF于点O，连接BF，由AB=AD，易证得△EOB∽△DOF，根据相似三角形的对应边成比例，可得 ，继而可证得△EOD∽△BOF，又由相似三角形的对应角相等，易得∠EBF=∠EFB=α，即可得EB=EF；（3）首先延长AB至G，使AG=AE，连接BE，GE，易证得△DEF∽△GBE，然后由相似三角形的对应边成比例，即可求得 的值．
【考点精析】解答此题的关键在于理解梯形的定义的相关知识，掌握一组对边平行，另一组对边不平行的四边形是梯形．两腰相等的梯形是等腰梯形，以及对相似三角形的判定与性质的理解，了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．