
【题目】如图所示,在数轴上点A,B,C表示得数为﹣2,0,6.点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,点A与点C之间的距离表示为AC.
(1)则AB= ,BC= ,AC= ;
(2)点A,B,C开始在数轴上运动,若点C以每秒3个单位长度向左运动,同时,点A和点B分别以每秒1个单位长度和每秒2个单位长度的速度向右运动,请问:t为何值时,AC=BC.请说明理由.
(3)点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动.
请问:BC﹣AB的值是否随着运动时间t的变化而变化?若变化,请说明理由;若不变,请求其值.
![]()
【答案】(1)2;6;8;(2)t为2秒时,AC=BC;(3)BC﹣AB的值不变,该值为6.
【解析】
(1)根据点A、B、C在数轴上的位置,写出AB、BC、AC的长度;
(2)分别表示出BC、AC的长度,当AC=BC求解即可.
(3)分别表示出AB、BC的长度,然后分情况讨论得出之间的关系.
解:(1)AB=0﹣(﹣2)=2,BC=6﹣0=6,AC=6﹣(﹣2)=8.
故答案为:2;6;8.
(2)当运动时间为t秒时,点A表示的数为t﹣2,点B表示的数为2t,点C表示的数为8﹣3t,则AC=|8﹣3t﹣(t﹣2)|=|10﹣4t|,BC=|8﹣3t﹣2t|=|8﹣5t|,
依题意,得:|10﹣4t|=|8﹣5t|,
解得:t1=﹣2(舍去),t2=2.
答:t为2秒时,AC=BC.
(3)当运动时间为t秒时,点A表示的数为﹣2﹣t,点B表示的数为2t,点C表示的数为8+5t,则BC=8+5t﹣2t=8+3t,AB=2t﹣(﹣2﹣t)=3t+2,
∴BC﹣AB=8+3t﹣(3t+2)=6,
∴BC﹣AB的值不变,该值为6.


科目:初中数学 来源: 题型:
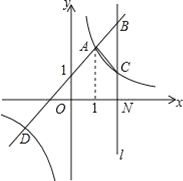
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(1)求一次函数与反比例函数的解析式;
(2)根据图象回答,x在什么范围内,一次函数的值大于反比例函数的值;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动,学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分如下:
课外阅读时间(单位:小时) | 频数(人数) | 频率 |
0<t≤2 | 2 | 0.04 |
2<t≤4 | 3 | 0.06 |
4<t≤6 | 15 | 0.30 |
6<t≤8 | a | 0.50 |
t>8 | 5 | b |
请根据图表信息回答下列问题:
(1)频数分布表中的a= ,b= ;
(2)将频数分布直方图补充完整;
(3)学校将每周课外阅读时间在8小时以上的学生评为“阅读之星”,请你估计该校2000名学生中评为“阅读之星”的有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解“阳光体育”活动的开展情况,从全校2000名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.

根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,m= ,n= ,表示区域C的圆心角为 度;
(3)全校学生中喜欢篮球的人数大约有 。
查看答案和解析>>
科目:初中数学 来源: 题型:
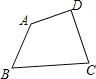
【题目】如图,已知四边形纸片ABCD,现将该纸片剪拼成一个与它面积相等的平行四边形纸片,如果限定裁剪线最多有两条,能否做到: (用“能”或“不能”填空).若“能”,请确定裁剪线的位置,并说明拼接方法;若填“不能”,请简要说明理由.方法或理由: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数:
﹣3.1,3.1415,﹣![]() ,+31,0.618,﹣
,+31,0.618,﹣![]() ,0,﹣1,﹣(﹣3),填在相应的集合里
,0,﹣1,﹣(﹣3),填在相应的集合里
分数集合: ;
整数集合: ;
非负整数集合: ;
正有理数集合: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com