
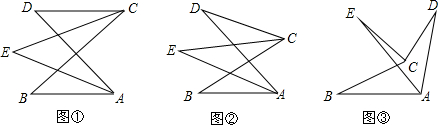
分析 (1)由三角形内角和定理,可得∠D+∠ECD=∠E+∠EAD,∠B+∠EAB=∠E+∠ECB,由角平分线的性质,可得∠ECD=∠ECB=$\frac{1}{2}$∠BCD,∠EAD=∠EAB=$\frac{1}{2}$∠BAD,则可得∠E=$\frac{1}{2}$(∠D+∠B),继而求得答案;
(2)由三角形内角和定理,可得∠D+∠ECD=∠E+∠EAD,∠B+∠EAB=∠E+∠ECB,由角平分线的性质,可得∠ECD=∠ECB=$\frac{1}{2}$∠BCD,∠EAD=∠EAB=$\frac{1}{2}$∠BAD,则可得∠E=$\frac{1}{2}$(∠D+∠B),继而求得答案;
(3)首先延长BC交AD于点F,由三角形外角的性质,可得∠BCD=∠B+∠BAD+∠D,又由角平分线的性质,即可求得答案.
解答 解:(1)∵CE平分∠BCD,AE平分∠BAD
∴∠ECD=∠ECB=$\frac{1}{2}$∠BCD,∠EAD=∠EAB=$\frac{1}{2}$∠BAD,
∵∠D+∠ECD=∠E+∠EAD,∠B+∠EAB=∠E+∠ECB,
∴∠D+∠ECD+∠B+∠EAB=∠E+∠EAD+∠E+∠ECB
∴∠D+∠B=2∠E,
∴∠E=$\frac{1}{2}$(∠D+∠B),
∵∠ADC=40°,∠ABC=30°,
∴∠AEC=$\frac{1}{2}$×(40°+30°)=35°;
(2)∵CE平分∠BCD,AE平分∠BAD
∴∠ECD=∠ECB=$\frac{1}{2}$∠BCD,∠EAD=∠EAB=$\frac{1}{2}$∠BAD,
∵∠D+∠ECD=∠E+∠EAD,∠B+∠EAB=∠E+∠ECB,
∴∠D+∠ECD+∠B+∠EAB=∠E+∠EAD+∠E+∠ECB
∴∠D+∠B=2∠E,
∴∠E=$\frac{1}{2}$(∠D+∠B),
∵∠ADC=m°,∠ABC=n°,
∴∠AEC=$\frac{m°+n°}{2}$;
∵∠E=$\frac{1}{2}$(∠D+∠B),∠B:∠D:∠E=2:4:x,
∴x=$\frac{1}{2}$(2+4)=3;
(3)延长BC交AD于点F,
∵∠BFD=∠B+∠BAD,
∴∠BCD=∠BFD+∠D=∠B+∠BAD+∠D,
∵CE平分∠BCD,AE平分∠BAD
∴∠ECD=∠ECB=$\frac{1}{2}$∠BCD,∠EAD=∠EAB=$\frac{1}{2}$∠BAD,
∵∠E+∠ECB=∠B+∠EAB,
∴∠E=∠B+∠EAB-∠ECB=∠B+∠BAE-$\frac{1}{2}$∠BCD=∠B+∠BAE-$\frac{1}{2}$(∠B+∠BAD+∠D)=$\frac{1}{2}$(∠B-∠D),
即∠AEC=$\frac{∠ABC-∠ADC}{2}$.
点评 此题考查了三角形内角和定理、三角形外角的性质以及角平分线的定义掌握角平分线的性质和等量代换是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1.5×200}{x}$-$\frac{240}{x}$=4 | B. | $\frac{240}{1.5x}$-$\frac{200}{4}$=4 | ||
| C. | $\frac{200}{x}$-$\frac{240}{1.5x}$=4 | D. | $\frac{1.5x+200}{x+4}$=$\frac{240}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,△ABO的三个顶点坐标分别为:A(2,3),B(3,1),O(0,0).
在平面直角坐标系中,△ABO的三个顶点坐标分别为:A(2,3),B(3,1),O(0,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
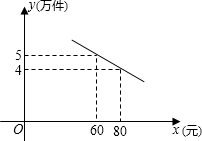 某通讯器材公司销售一种市场需求较大的新型通讯产品,已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120万元,在销售过程中发现,年销售量y(万件)与销售单价x(元)之间存在着如图所示的一次函数关系.
某通讯器材公司销售一种市场需求较大的新型通讯产品,已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120万元,在销售过程中发现,年销售量y(万件)与销售单价x(元)之间存在着如图所示的一次函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
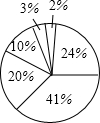 根据如图的数据制作扇形统计图并回答问题
根据如图的数据制作扇形统计图并回答问题查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com