
【题目】已知:如图,在平行四边形ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.
(1)说明△DCE≌△FBE的理由;
(2)若EC=3,求AD的长.

【答案】(1)证明见解析(2)6
【解析】
(1)由四边形ABCD是平行四边形,根据平行四边形的对边平行且相等,即可得AB=DC,AB∥DC,继而可求得∠CDE=∠F,又由BF=AB,即可利用AAS,判定△DCE≌△FBE.
(2)由(1),可得BE=EC,即可求得BC的长,又由平行四边形的对边相等,即可求得AD的长
(1)证明:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC.
∴∠CDE=∠F.
又∵BF=AB,
∴DC=FB.
在△DCE和△FBE中,
∵∠CDE=∠F,∠CED=∠BEF, DC=FB,
∴△DCE≌△FBE(AAS).
(2)解:∵△DCE≌△FBE,
∴EB=EC.
∵EC=3,
∴BC=2EB=6.
∵四边形ABCD是平行四边形,
∴AD=BC.
∴AD=6


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
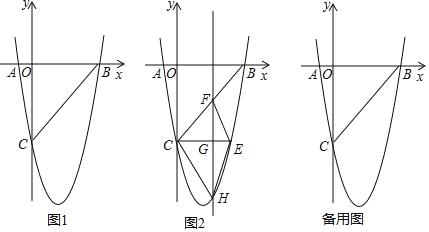
【题目】如图 1,在平面直角坐标系中,已知抛物线 y=ax2+bx﹣5 与 x 轴交于 A(﹣1,0),B(5, 0)两点,与 y 轴交于点 C.
(1)求抛物线的函数表达式;
(2)若点 D 是 y 轴上的一点,且以 B,C,D 为顶点的三角形与△ABC 相似,求点 D 的坐标;
(3)如图 2,CE∥x 轴与抛物线相交于点 E,点 H 是直线 CE 下方抛物线上的动点,过点 H且与 y 轴平行的直线与 BC,CE 分别相交于点 F,G,试探究当点 H 运动到何处时,四边形CHEF 的面积最大,求点 H 的坐标及最大面积;
(4)若点 K 为抛物线的顶点,点 M(4,m)是该抛物线上的一点,在 x 轴,y 轴上分别找点 P,Q,使四边形 PQKM 的周长最小,求出点 P,Q 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,F为AB上一点,E是BC延长线上一点,且AF=EC,连接EF,DE,DF,M是FE中点,连结MC,设FE与DC相交于点N.则4个结论:①DN=DG;②△BFG∽△EDG∽△BDE;③CM垂直BD;④若MC=![]() ,则BF=2;正确的结论有( )个
,则BF=2;正确的结论有( )个
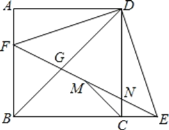
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
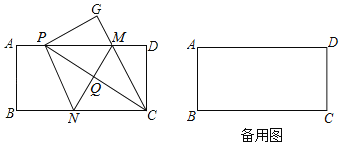
【题目】如图,现有一张矩形纸片ABCD,AB=4,BC=8,点M,N分别在矩形的边AD,BC上,将矩形纸片沿直线MN折叠,使点C落在矩形的边AD上,记为点P,点D落在G处,连接PC,交MN丁点Q,连接CM.
(1)求证:PM=PN;
(2)当P,A重合时,求MN的值;
(3)若△PQM的面积为S,求S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
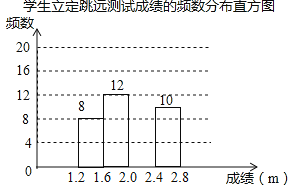
【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x<1.6 | a |
1.6≤x<2.0 | 12 |
2.0≤x<2.4 | b |
2.4≤x<2.8 | 10 |
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个批发店销售同一种苹果,在甲批发店,不论一次购买数量是多少,价格均为6元/![]() .在乙批发店,一次购买数量不超过
.在乙批发店,一次购买数量不超过![]() 时,价格为7元/
时,价格为7元/![]() ;一次购买数量超过
;一次购买数量超过![]() 时,其中有
时,其中有![]() 的价格仍为7元/
的价格仍为7元/![]() ,超过
,超过![]() 部分的价格为5元/
部分的价格为5元/![]() .设小王在同一个批发店一次购买苹果的数量为
.设小王在同一个批发店一次购买苹果的数量为![]() .
.
(Ⅰ)根据题意填空:
①若一次购买数量为![]() 时,在甲批发店的花费为________元,在乙批发店的花费为________元;
时,在甲批发店的花费为________元,在乙批发店的花费为________元;
②若一次购买数量为![]() 时,在甲批发店的花费为________元,在乙批发店的花费为________元;
时,在甲批发店的花费为________元,在乙批发店的花费为________元;
(Ⅱ)设在甲批发店花费![]() 元,在乙批发店花费
元,在乙批发店花费![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(Ⅲ)根据题意填空:
①若小王在甲批发店和在乙批发店一次购买苹果的数量相同,且花费相同,则他在同一个批发店一次购买苹果的数量为_________![]() ;
;
②若小王在同一个批发店一次购买苹果的数量为![]() ,则他在甲、乙两个批发店中的________批发店购买花费少;
,则他在甲、乙两个批发店中的________批发店购买花费少;
③若小王在同一个批发店一次购买苹果花费了260元,则他在甲、乙两个批发店中的_________批发店购买数量多.
查看答案和解析>>
科目:初中数学 来源: 题型:
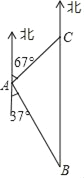
【题目】如图,在港口A的南偏东37°方向的海面上,有一巡逻艇B,A、B相距20海里,这时在巡逻艇的正北方向及港口A的北偏东67°方向上,有一渔船C发生故障.得知这一情况后,巡逻艇以25海里/小时的速度前往救援,问巡逻艇能否在1小时内到达渔船C处?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图像如图所示,则下列结论正确的个数有( )
①c>0;②b2-4ac<0;③ a-b+c>0;④当x>-1时,y随x的增大而减小.
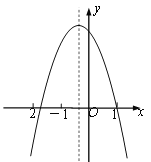
A.4个B.3个C.2个D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com