
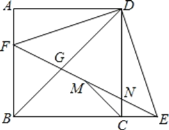
【题目】如图,正方形ABCD中,F为AB上一点,E是BC延长线上一点,且AF=EC,连接EF,DE,DF,M是FE中点,连结MC,设FE与DC相交于点N.则4个结论:①DN=DG;②△BFG∽△EDG∽△BDE;③CM垂直BD;④若MC=![]() ,则BF=2;正确的结论有( )个
,则BF=2;正确的结论有( )个
A.4B.3C.2D.1
【答案】B
【解析】
根据正方形的性质可得AD=CD,然后利用“边角边”证明△ADF和△CDE全等,根据全等三角形对应角相等可得∠ADF=∠CDE,然后求出∠EDF=∠ADC=90°,而∠DGN=45°+∠FDG,∠DNG=45°+∠CDE,∠FDG不一定等于∠CDE,于是∠DGN不一定等于∠DNG,判断出①错误;
根据全等三角形对应边相等可得DE=DF,然后判断出△DEF是等腰直角三角形,根据等腰直角三角形的性质可得∠DEF=45°,再根据两组角对应相等的三角形相似得到△BFG∽△EDG∽△BDE,判断出②正确;
连接BM、DM,根据直角三角形斜边上的中线等于斜边的一半可得![]() 然后判断出直线CM垂直平分BD,判断出③正确;
然后判断出直线CM垂直平分BD,判断出③正确;
过点M作MH⊥BC于H,得到∠MCH=45°,然后求出MH,再根据三角形的中位线平行于第三边并且等于第三边的一半可得BF=2MH,判断出④正确.
在正方形ABCD中,AD=CD,
在△ADF和△CDE中,
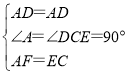 ,
,
∴△ADF≌△CDE(SAS),
∴∠ADF=∠CDE,DE=DF,
∴∠EDF=∠FDC+∠CDE=∠FDC+∠ADF=∠ADC=90°,
∴∠DEF=45°,
∵∠DGN=45°+∠FDG,∠DNG=45°+∠CDE,∠FDG≠∠CDE,
而∠FDG与∠CDE不一定相等,
∴∠DGN与∠DNG不一定相等,故判断出①错误;
∵△DEF是等腰直角三角形,
∵∠ABD=∠DEF=45°,∠BGF=∠EGD(对顶角相等),
∴△BFG∽△EDG,
∵∠DBE=∠DEF=45°,∠BDE=∠EDG,
∴△EDG∽△BDE,
∴△BFG∽△EDG∽△BDE,故②正确;
如图,连接BM、DM
.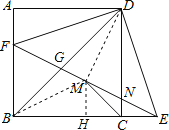
∵△AFD≌△CED,
∴∠FDA=∠EDC,DF=DE,
∴∠FDE=∠ADC=90°,
∵M是EF的中点,
∴![]()
∵![]()
∴MD=MB,
在△DCM与△BCM中,
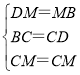 ,
,
∴△DCM≌△BCM(SSS),
∴∠BCM=∠DCM,
∴CM在正方形ABCD的角平分线AC上,
∴MC垂直平分BD;故③正确;
过点M作MH⊥BC于H,则∠MCH=45°,
∵![]() ,
,
∴![]() ,
,
∵M是EF的中点,BF⊥BC,MH⊥BC,
∴MH是△BEF的中位线,
∴BF=2MH=2,故④正确;
综上所述,正确的结论有②③④.
故选:B.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数y=2x+b的图象与x轴的交点为A(2,0),与y轴的交点为B,直线AB与反比例函数y=![]() 的图象交于点C(﹣1,m).
的图象交于点C(﹣1,m).
(1)求一次函数和反比例函数的表达式;
(2)直接写出关于x的不等式2x+b>![]() 的解集;
的解集;
(3)点P是这个反比例函数图象上的点,过点P作PM⊥x轴,垂足为点M,连接OP,BM,当S△ABM=2S△OMP时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来网约车十分流行,初三某班学生对“美团”和“滴滴”两家网约车公司各10名司机月收入进行了一项抽样调查,司机月收入(单位:千元)如图所示:

根据以上信息,整理分析数据如下:
平均月收/千元 | 中位数/千元 | 众数/千元 | 方差/千元 | |
“美团” | ① | 6 | 6 | 1.2 |
“滴滴” | 6 | ② | 4 | ③ |
(1)完成表格填空:①__________②__________③__________
(2)若从两家公司中选择一家做网约车司机,你会选哪家公司,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
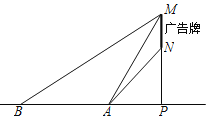
【题目】某数学社团成员想利用所学的知识测量某广告牌的宽度![]() 图中线段MN的长
图中线段MN的长![]() ,直线MN垂直于地面,垂足为点
,直线MN垂直于地面,垂足为点![]() 在地面A处测得点M的仰角为
在地面A处测得点M的仰角为![]() 、点N的仰角为
、点N的仰角为![]() ,在B处测得点M的仰角为
,在B处测得点M的仰角为![]() ,
,![]() 米,且A、B、P三点在一直线上
米,且A、B、P三点在一直线上![]() 请根据以上数据求广告牌的宽MN的长.
请根据以上数据求广告牌的宽MN的长.
![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是边长为
是边长为![]() 的等边三角形,边
的等边三角形,边![]() 在射线
在射线![]() 上,且
上,且![]() ,点
,点![]() 从点
从点![]() 出发,沿OM的方向以1cm/s的速度运动,当D不与点A重合时,将
出发,沿OM的方向以1cm/s的速度运动,当D不与点A重合时,将![]() 绕点C逆时针方向旋转60°得到
绕点C逆时针方向旋转60°得到![]() ,连接DE.
,连接DE.
(1)如图1,求证:![]() 是等边三角形;
是等边三角形;
(2)如图2,当6<t<10时,DE是否存在最小值?若存在,求出DE的最小值;若不存在,请说明理由.
(3)当点D在射线OM上运动时,是否存在以D,E,B为顶点的三角形是直角三角形?若存在,求出此时t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数-3,1.
(1)在下列数轴上,标出表示这两个数的点,并分别用A,B表示;
(2)若|m|=2,在数轴上表示数m的点,介于点A,B之间,在A的右侧且到点B距离为5的点表示为n.
①计算m+n-mn;
②解关于x的不等式mx+4<n,并把解集表示在下列数轴上.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.
(1)说明△DCE≌△FBE的理由;
(2)若EC=3,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
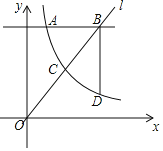
【题目】如图,反比例函数y=![]() (x>0)的图象与直线y=mx交于点C,直线l:y=4分别交两函数图象于点A(1,4)和点B,过点B作BD⊥l交反比例函数图象于点 D.
(x>0)的图象与直线y=mx交于点C,直线l:y=4分别交两函数图象于点A(1,4)和点B,过点B作BD⊥l交反比例函数图象于点 D.
(1)求反比例函数的解析式;
(2)当BD=2AB时,求点B的坐标;
(3)在(2)的条件下,直接写出不等式![]() >mx的解集.
>mx的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com