
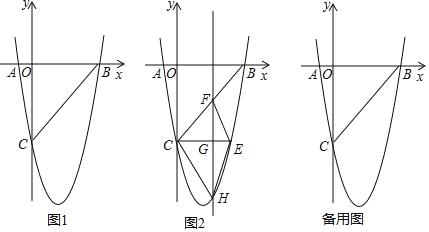
【题目】如图 1,在平面直角坐标系中,已知抛物线 y=ax2+bx﹣5 与 x 轴交于 A(﹣1,0),B(5, 0)两点,与 y 轴交于点 C.
(1)求抛物线的函数表达式;
(2)若点 D 是 y 轴上的一点,且以 B,C,D 为顶点的三角形与△ABC 相似,求点 D 的坐标;
(3)如图 2,CE∥x 轴与抛物线相交于点 E,点 H 是直线 CE 下方抛物线上的动点,过点 H且与 y 轴平行的直线与 BC,CE 分别相交于点 F,G,试探究当点 H 运动到何处时,四边形CHEF 的面积最大,求点 H 的坐标及最大面积;
(4)若点 K 为抛物线的顶点,点 M(4,m)是该抛物线上的一点,在 x 轴,y 轴上分别找点 P,Q,使四边形 PQKM 的周长最小,求出点 P,Q 的坐标.
【答案】(1)y=x2﹣4x﹣5;(2)D 的坐标为(0,1)或(0,![]() );(3)H(
);(3)H(![]() ,﹣
,﹣![]() ),S=
),S=![]() ;(4)P(
;(4)P(![]() ,0),Q(0,﹣
,0),Q(0,﹣![]() ).
).
【解析】
(1)根据待定系数法直接确定出抛物线解析式;
(2)分两种情况,利用相似三角形的比例式即可求出点 D 的坐标;
(3)先求出直线 BC 的解析式,进而求出四边形 CHEF 的面积的函数关系式,即可求出最大值;
(4)利用对称性找出点 P,Q 的位置,进而求出 P,Q 的坐标.
(1)∵点 A(﹣1,0),B(5,0)在抛物线 y=ax2+bx﹣5 上,
∴![]() ,
,
∴![]() ,
,
∴抛物线的表达式为 y=x2﹣4x﹣5,
(2)如图 1,
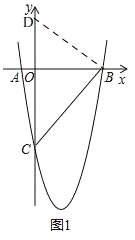
令 x=0,则 y=﹣5,
∴C(0,﹣5),
∴OC=OB,
∴∠OBC=∠OCB=45°,
∴AB=6,BC=5![]() ,
,
要使以 B,C,D 为顶点的三角形与△ABC 相似,则![]() 或
或![]() ,
,
①![]() 时,
时,
CD=AB=6,
∴D(0,1),
②当![]() 时,
时,
∴![]() ,
,
∴CD=![]() ,
,
∴D(0,![]() ),
),
即:D的坐标为(0,1)或(0,![]() );
);
(3)设 H(t,t2﹣4t﹣5),
∵CE∥x轴,
∴点E的纵坐标为﹣5,
∵E在抛物线上,
∴x2﹣4x﹣5=﹣5,
∴x=0(舍)或 x=4,
∴E(4,﹣5),
∴CE=4,
∵B(5,0),C(0,﹣5),
∴直线BC的解析式为y=x﹣5,
∴F(t,t﹣5),
∴HF=t﹣5﹣(t2﹣4t﹣5)=﹣(t﹣![]() )2+
)2+![]() ,
,
∵CE∥x轴,HF∥y轴,
∴CE⊥HF,
∴S四边形CHEF=![]() CEHF=﹣2(t﹣
CEHF=﹣2(t﹣![]() )2+
)2+![]() ,
,
当t=![]() 时,四边形CHEF的面积最大
时,四边形CHEF的面积最大![]() .
.
当t=![]() 时,t2-4t-5=
时,t2-4t-5=![]() ﹣10﹣5=﹣
﹣10﹣5=﹣![]() ,
,
∴H(![]() ,﹣
,﹣![]() );
);
(4)如图 2,
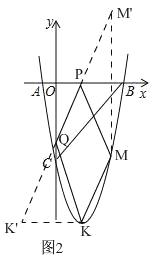
∵K 为抛物线的顶点,
∴K(2,﹣9),
∴K 关于 y 轴的对称点 K'(﹣2,﹣9),
∵M(4,m)在抛物线上,
∴M(4,﹣5),
∴点 M 关于 x 轴的对称点 M'(4,5),
∴直线 K'M'的解析式为 ![]() x﹣
x﹣![]() ,
,
∴P(![]() ,0),Q(0,﹣
,0),Q(0,﹣![]() ).
).


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,我们把以抛物线![]() 上的动点A为顶点的抛物线叫做这条抛物线的“子抛物线”.如图,已知某条“子抛物线”的二次项系数为
上的动点A为顶点的抛物线叫做这条抛物线的“子抛物线”.如图,已知某条“子抛物线”的二次项系数为![]() ,且与y轴交于点C.设点A的横坐标为m(m>0),过点A作y轴的垂线交y轴于点B.
,且与y轴交于点C.设点A的横坐标为m(m>0),过点A作y轴的垂线交y轴于点B.
(1)当m=1时,求这条“子抛物线”的解析式;
(2)用含m的代数式表示∠ACB的余切值;
(3)如果∠OAC=135°,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数y=2x+b的图象与x轴的交点为A(2,0),与y轴的交点为B,直线AB与反比例函数y=![]() 的图象交于点C(﹣1,m).
的图象交于点C(﹣1,m).
(1)求一次函数和反比例函数的表达式;
(2)直接写出关于x的不等式2x+b>![]() 的解集;
的解集;
(3)点P是这个反比例函数图象上的点,过点P作PM⊥x轴,垂足为点M,连接OP,BM,当S△ABM=2S△OMP时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
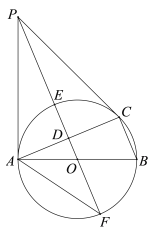
【题目】如图,⊙O是△ABC的外接圆,AB是直径,D是AC中点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接PA,PC,AF,且满足∠PCA=∠ABC.
(1)求证:PA是⊙O的切线;
(2)证明:![]() ;
;
(3)若BC=8,tan∠AFP=![]() ,求DE的长.
,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
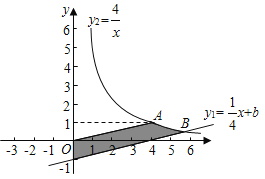
【题目】在平面直角坐标系中,点![]() ,直线
,直线![]() 与双曲线
与双曲线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .探究:由双曲线
.探究:由双曲线![]() 与线段
与线段![]() 围成的区域
围成的区域![]() 内(不含边界)整点的个数(点的横、纵坐标都是整数的点称为整点).①当
内(不含边界)整点的个数(点的横、纵坐标都是整数的点称为整点).①当![]() 时,如图,区域
时,如图,区域![]() 内的整点的个数为_____;②若区域
内的整点的个数为_____;②若区域![]() 内恰有4个整点,结合函数图象,则
内恰有4个整点,结合函数图象,则![]() 的取值范围是_______
的取值范围是_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来网约车十分流行,初三某班学生对“美团”和“滴滴”两家网约车公司各10名司机月收入进行了一项抽样调查,司机月收入(单位:千元)如图所示:

根据以上信息,整理分析数据如下:
平均月收/千元 | 中位数/千元 | 众数/千元 | 方差/千元 | |
“美团” | ① | 6 | 6 | 1.2 |
“滴滴” | 6 | ② | 4 | ③ |
(1)完成表格填空:①__________②__________③__________
(2)若从两家公司中选择一家做网约车司机,你会选哪家公司,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
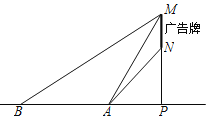
【题目】某数学社团成员想利用所学的知识测量某广告牌的宽度![]() 图中线段MN的长
图中线段MN的长![]() ,直线MN垂直于地面,垂足为点
,直线MN垂直于地面,垂足为点![]() 在地面A处测得点M的仰角为
在地面A处测得点M的仰角为![]() 、点N的仰角为
、点N的仰角为![]() ,在B处测得点M的仰角为
,在B处测得点M的仰角为![]() ,
,![]() 米,且A、B、P三点在一直线上
米,且A、B、P三点在一直线上![]() 请根据以上数据求广告牌的宽MN的长.
请根据以上数据求广告牌的宽MN的长.
![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.
(1)说明△DCE≌△FBE的理由;
(2)若EC=3,求AD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com