
【题目】在平面直角坐标系xOy中,我们把以抛物线![]() 上的动点A为顶点的抛物线叫做这条抛物线的“子抛物线”.如图,已知某条“子抛物线”的二次项系数为
上的动点A为顶点的抛物线叫做这条抛物线的“子抛物线”.如图,已知某条“子抛物线”的二次项系数为![]() ,且与y轴交于点C.设点A的横坐标为m(m>0),过点A作y轴的垂线交y轴于点B.
,且与y轴交于点C.设点A的横坐标为m(m>0),过点A作y轴的垂线交y轴于点B.
(1)当m=1时,求这条“子抛物线”的解析式;
(2)用含m的代数式表示∠ACB的余切值;
(3)如果∠OAC=135°,求m的值.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)m的值为2
;(3)m的值为2
【解析】
(1)先求出m=1时点A的坐标,进而可得到这条“子抛物线”的解析式;
(2)先根据A点坐标求出“子抛物线”的解析式和AB,OB的长度,然后令x = 0求出y值即可得到C点坐标,进而可求出BC的长度,最后利用![]() 即可求解;
即可求解;
(3)过O点作OD⊥CA的延长线于点D,过点D作y轴的平行线分别交BA的延长线于点E,交x轴于点F, 首先证明△AED≌△DFO,则有AE=DF,DE=OF,设AE=n,那么DF=n,BE= m + n=OF=ED,通过OB=EF得到![]() ,然后再通过
,然后再通过![]() 得到
得到![]() ,将两个关于m,n的方程联立即可求出m的值.
,将两个关于m,n的方程联立即可求出m的值.
解:(1)∵点A在![]() 上,点A的横坐标为m,
上,点A的横坐标为m,
∴A(m,m2),
当m =1时,![]() ,
,
∴A(1,1),
∴这条“子抛物线”的解析式为![]() .
.
(2)由A(m,m2),且AB⊥y轴,可得AB=m,OB= m2.
∴“子抛物线”的解析式为![]() .
.
令x = 0,![]() ,
,
∴点C的坐标(0,![]() ),
),![]() ,
,
∴![]() .
.
在Rt△ABC中,
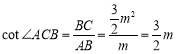 .
.
(3)如图,过O点作OD⊥CA的延长线于点D,过点D作y轴的平行线分别交BA的延长线于点E,交x轴于点F.
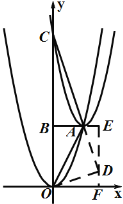
∵∠OAC=135°,
∴∠OAD=45°.
又∵OD⊥CA,
![]()
∴∠AOD=∠OAD=45°,
∴AD=OD,
![]() ,
,
![]() .
.
![]() ,
,
∴△AED≌△DFO,
∴AE=DF,DE=OF.
设AE=n,那么DF=n,BE= m + n=OF=ED.
又∵OB=EF,
∴![]() .
.
又![]() ,
,
∴∠BCA=∠ADE,
∴![]() .
.
解方程组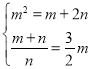 ,得
,得![]() ,
,![]() (舍去)
(舍去)
∴ m的值为2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,点P、Q分别在BC、CD上,∠PAQ=∠B.
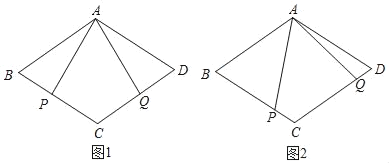
(1)如图1,若AP⊥BC,求证:AP=AQ;
(2)如图2,若点P为BC上一点,AP=AQ仍成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
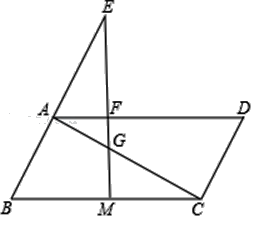
【题目】已知,如图,在平行四边形ABCD中,M是BC边的中点,E是边BA延长线上的一点,连结EM,分别交线段AD、AC于点F、G.
(1)求证:![]() ;
;
(2)当BC2=2BABE时,求证:∠EMB=∠ACD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,按以下步骤作图:
①分别以点C和点D为圆心,大于![]() 的同样的长为半径作弧,两弧交于M,N两点;
的同样的长为半径作弧,两弧交于M,N两点;
②作直线MN,交CD于点E,连接BE.
若直线MN恰好经过点A,则下列说法错误的是( )
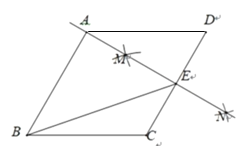
A.ABC60°
B.![]()
C.若AB4,则BE![]()
D.tanCBE![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于任意两点
中,对于任意两点![]() ,
,![]() ,如果
,如果![]() ,则称
,则称![]() 与
与![]() 互为“
互为“![]() 距点”.例如:点
距点”.例如:点![]() ,点
,点![]() ,由
,由![]() ,可得点
,可得点![]() 与
与![]() 互为“
互为“![]() 距点”.
距点”.
(1)在点![]() ,
,![]() ,
,![]() 中,原点
中,原点![]() 的“
的“![]() 距点”是_____(填字母);
距点”是_____(填字母);
(2)已知点![]() ,点
,点![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() .
.
①当![]() 时,直线
时,直线![]() 上点
上点![]() 的“
的“![]() 距点”的坐标为_____;
距点”的坐标为_____;
②若直线![]() 上存在点
上存在点![]() 的“
的“![]() 点”,求
点”,求![]() 的取值范围.
的取值范围.
(3)已知点![]() ,
,![]() ,
,![]() ,
,![]() 的半径为
的半径为![]() ,若在线段
,若在线段![]() 上存在点
上存在点![]() ,在
,在![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 与点
与点![]() 互为“
互为“![]() 距点”,直接写出
距点”,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于两个不相等的实数a,b,我们规定符号max{a,b}表示a、b中的较大的数,如:max{2,4}=4,按照这个规定,方程max{x,﹣x}=x2﹣x﹣1的解为( )
A.1+![]() 或1﹣
或1﹣![]() B.1或﹣1C.1﹣
B.1或﹣1C.1﹣![]() 或1D.1+
或1D.1+![]() 或﹣1
或﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
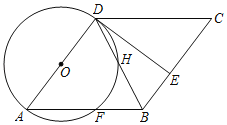
【题目】如图,四边形ABCD为菱形,以AD为直径作⊙O交AB于点F,连接DB交⊙O于点H,E是BC上的一点,且BE=BF,连接DE.
(1)求证:△DAF≌△DCE.
(2)求证:DE是⊙O的切线.
(3)若BF=2,DH=![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在读书月活动中,学校准备购买一批课外读物,为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:

(1)本次调查中,一共调查了_____名同学;
(2)条形统计图中,m=_____,n=_______;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是______度;
(4)学校计划购买课外读物5000册,请根据样本数据,估计学校购买其他类读物多少册比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
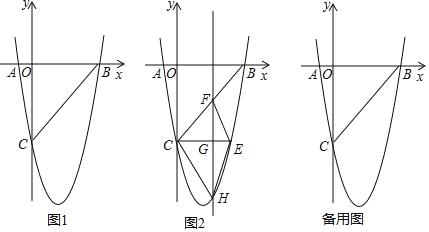
【题目】如图 1,在平面直角坐标系中,已知抛物线 y=ax2+bx﹣5 与 x 轴交于 A(﹣1,0),B(5, 0)两点,与 y 轴交于点 C.
(1)求抛物线的函数表达式;
(2)若点 D 是 y 轴上的一点,且以 B,C,D 为顶点的三角形与△ABC 相似,求点 D 的坐标;
(3)如图 2,CE∥x 轴与抛物线相交于点 E,点 H 是直线 CE 下方抛物线上的动点,过点 H且与 y 轴平行的直线与 BC,CE 分别相交于点 F,G,试探究当点 H 运动到何处时,四边形CHEF 的面积最大,求点 H 的坐标及最大面积;
(4)若点 K 为抛物线的顶点,点 M(4,m)是该抛物线上的一点,在 x 轴,y 轴上分别找点 P,Q,使四边形 PQKM 的周长最小,求出点 P,Q 的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com