
【题目】在菱形ABCD中,点P、Q分别在BC、CD上,∠PAQ=∠B.
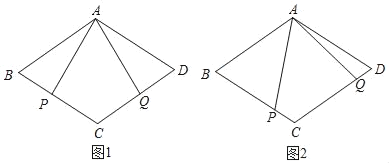
(1)如图1,若AP⊥BC,求证:AP=AQ;
(2)如图2,若点P为BC上一点,AP=AQ仍成立吗?请说明理由.
【答案】(1)成立;(2)成立,见解析
【解析】
(1)根据题意可利用菱形的性质证明△ABP≌△ADQ(AAS)即可解答
(2)过点A作AE⊥BC于点E,AF⊥CD于点F,在证明△AEP≌△AFQ(ASA)即可解答
(1)在菱形ABCD中,
∠B+∠C=180°,AB=AD,∠B=∠D,
∵∠PAQ=∠B,
∴∠PAQ+∠C=180°,
∴∠APC+∠AQC=180°,
∵AP⊥BC,
∴∠APB=∠AQD=90°,
在△ABP与△ADQ中,
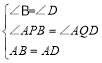 ,
,
∴△ABP≌△ADQ(AAS),
∴AP=AQ;
(2)过点A作AE⊥BC于点E,AF⊥CD于点F,
由(1)可知:AE=AF,∠PAQ=∠B=∠EAF,
∴∠EAP=∠FAQ,
在△AEP与△AFQ中,
![]()
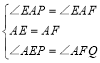 ,
,
∴△AEP≌△AFQ(ASA),
∴AP=AQ.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】陕西省相关文件规定,西安市实行居民阶梯水价制度,对居民用水的基本水价实行![]() 三级价差,各阶梯水价均为用户终端水价,具体如下:
三级价差,各阶梯水价均为用户终端水价,具体如下:
第一阶梯:年用水量![]() 及以下,终端水价为
及以下,终端水价为![]() 元/
元/![]() .
.
第二阶梯:年用水量![]() (含),终端水价为
(含),终端水价为![]() 元/
元/![]() .
.
第三阶梯:年用水量![]() 以上,终端水价为
以上,终端水价为![]() 元/
元/![]() .
.
城区居民阶梯水价计量结算周期以年为单位,年用水量累计达到各阶梯水量上限后,超出部分执行下一阶梯水价;年度周期之间水量不结转,不累计.
设某户居民2019年的年用水量为![]() ,应缴水费为
,应缴水费为![]() (元).
(元).
(1)写出该户居民2019年的年用水量为![]() 含)的
含)的![]() 与
与![]() 之间的函数表达式.
之间的函数表达式.
(2)若该户居民2019年的应缴水费为![]() 元,则该户居民2019年的年用水量为多少.
元,则该户居民2019年的年用水量为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=3x﹣5与反比例函数y2=![]() 的图象相交A(2,m),B(n,﹣6)两点,连接OA,OB.
的图象相交A(2,m),B(n,﹣6)两点,连接OA,OB.
(1)求k和n的值;
(2)求△AOB的面积;
(3)直接写出y1> y2时自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年五月,我国南方某省A、B两市遭受严重洪涝灾害,邻近县市C、D决定调运物资支援A、B两市灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市,A市需要的物资比B市需要的物资少100吨.已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用分别为每吨15元和30元,设从D市运往B市的救灾物资为x吨.
(1)A、B两市各需救灾物资多少吨?
(2)设C、D两市的总运费为w元,求w与x之间的函数关系式,并写出自变量x的取值范围;
(3)经过抢修,从D市到B市的路况得到了改善,缩短了运输时间,运费每吨减少m元(m>0),其余路线运费不变.若C、D两市的总运费的最小值不小于10320元,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
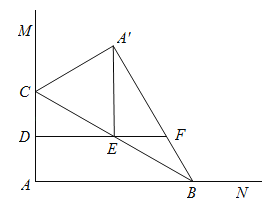
【题目】如图,![]() 点
点![]() 在边
在边![]() 上,
上,![]() 点
点![]() 为边
为边![]() 上一动点,连接
上一动点,连接![]() 与
与![]() 关于
关于![]() 所在直线对称,点
所在直线对称,点![]() 分别为
分别为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 所在直线于点
所在直线于点![]() ,连接
,连接![]() .当
.当![]() 为直角三角形时,
为直角三角形时,![]() 的长为_________ .
的长为_________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
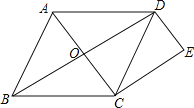
【题目】如图,点O是菱形ABCD对角线的交点,过点C作CE∥OD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形OCED是矩形.
(2)若AB=4,∠ABC=60°,求矩形OCED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点,作BM⊥AE于点M,作KN⊥AE于点N,连结MO、NO,以下四个结论:①△OMN是等腰三角形;②tan∠OMN=![]() ;③BP=4PK;④PMPA=3PD2,其中正确的是( )
;③BP=4PK;④PMPA=3PD2,其中正确的是( )
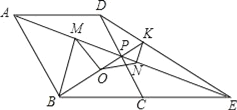
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形纸片![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的动点(点
边上的动点(点![]() 不与点
不与点![]() 、
、![]() 重合),如图1所示,沿折痕
重合),如图1所示,沿折痕![]() 翻折得到
翻折得到![]() ,设
,设![]() .
.
(1)当![]() 、
、![]() 、
、![]() 在同一直线上时,求
在同一直线上时,求![]() 的值;
的值;
(2)如图2,点![]() 在
在![]() 边上,沿
边上,沿![]() 再次折叠纸片,使点
再次折叠纸片,使点![]() 的对应点
的对应点![]() 在直线
在直线![]() 上,
上,
①求![]() 的最小值;
的最小值;
②点![]() 能否落在边
能否落在边![]() 上?若能,求出
上?若能,求出![]() 的值,若不能,试说明理由.
的值,若不能,试说明理由.
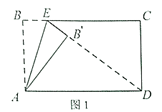

查看答案和解析>>
科目:初中数学 来源: 题型:
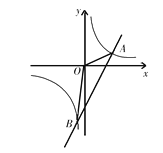
【题目】在平面直角坐标系xOy中,我们把以抛物线![]() 上的动点A为顶点的抛物线叫做这条抛物线的“子抛物线”.如图,已知某条“子抛物线”的二次项系数为
上的动点A为顶点的抛物线叫做这条抛物线的“子抛物线”.如图,已知某条“子抛物线”的二次项系数为![]() ,且与y轴交于点C.设点A的横坐标为m(m>0),过点A作y轴的垂线交y轴于点B.
,且与y轴交于点C.设点A的横坐标为m(m>0),过点A作y轴的垂线交y轴于点B.
(1)当m=1时,求这条“子抛物线”的解析式;
(2)用含m的代数式表示∠ACB的余切值;
(3)如果∠OAC=135°,求m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com