
【题目】在平面直角坐标系中,点![]() ,直线
,直线![]() 与双曲线
与双曲线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .探究:由双曲线
.探究:由双曲线![]() 与线段
与线段![]() 围成的区域
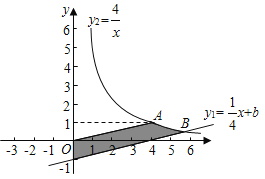
围成的区域![]() 内(不含边界)整点的个数(点的横、纵坐标都是整数的点称为整点).①当
内(不含边界)整点的个数(点的横、纵坐标都是整数的点称为整点).①当![]() 时,如图,区域
时,如图,区域![]() 内的整点的个数为_____;②若区域
内的整点的个数为_____;②若区域![]() 内恰有4个整点,结合函数图象,则
内恰有4个整点,结合函数图象,则![]() 的取值范围是_______
的取值范围是_______
【答案】3 ![]() 或
或![]() .
.
【解析】
①将![]() 时代入可得:直线解析式为
时代入可得:直线解析式为![]() ,画图可得整点的个数;
,画图可得整点的个数;
②分两种情况:直线![]() 在OA的下方和上方,画图计算边界时点b的值,可得b的取值.
在OA的下方和上方,画图计算边界时点b的值,可得b的取值.
①当![]() 时,则直线
时,则直线![]() ,
,
解方程![]() 得:
得:![]() (舍去),
(舍去),
∴点B的坐标为(![]() ,
,![]() ),
),
令![]() ,则
,则![]() ,得:
,得:![]() ,
,
经过点(![]() ,
,![]() ),
),
观察图形,可知:
区域M内的整点有(1,0),(2,0),(3,0),有3个,
故答案为:3;
②当直线![]() 在OA下方时,
在OA下方时,
过点(1,-1)时,![]() ,
,![]() ,
,
∴直线的解析式为![]() ,
,
令![]() ,则
,则![]() ,得:
,得:![]() ,
,
经过点(![]() ,
,![]() ),
),
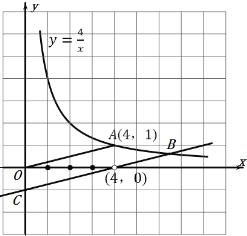
作出图象如图所示:

观察图象可知:当![]() 时,区域M内的整点有4个,分别是:(1,0),(2,0),(3,0),(4,0);
时,区域M内的整点有4个,分别是:(1,0),(2,0),(3,0),(4,0);
当直线![]() 在OA上方时,
在OA上方时,
∵点(2,2)在函数![]() 的图象上,
的图象上,
当直线![]() 过(1,2)时,
过(1,2)时,![]() ,
,
∴直线的解析式为![]() ,
,
当直线![]() 过(1,3)时,
过(1,3)时,![]() ,
,
∴直线的解析式为 ![]() ,
,
作出图象如图所示:
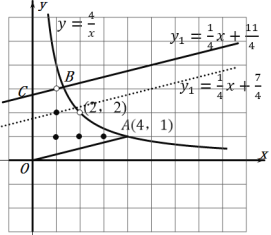
观察图象可知:当![]() 时,区域M内的整点有4个,分别是:(1,1),(1,2),(2,1),(3,1);
时,区域M内的整点有4个,分别是:(1,1),(1,2),(2,1),(3,1);
综上所述,区域M内恰有4个整点,b的取值范围是:![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】对于两个不相等的实数a,b,我们规定符号max{a,b}表示a、b中的较大的数,如:max{2,4}=4,按照这个规定,方程max{x,﹣x}=x2﹣x﹣1的解为( )
A.1+![]() 或1﹣
或1﹣![]() B.1或﹣1C.1﹣
B.1或﹣1C.1﹣![]() 或1D.1+
或1D.1+![]() 或﹣1
或﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
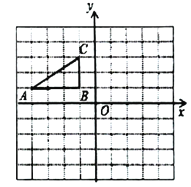
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形.![]() 的顶点均在格点上,建立平面直角坐标系后,点
的顶点均在格点上,建立平面直角坐标系后,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)先将![]() 向右平移5个单位,再向下平移1个单位后得到
向右平移5个单位,再向下平移1个单位后得到![]() .试在图中画出图形
.试在图中画出图形![]() ,并写出
,并写出![]() 的坐标;
的坐标;
(2)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后得到
后得到![]() ,试在图中画出图形
,试在图中画出图形![]() .并计算在该旋转过程中
.并计算在该旋转过程中![]() 扫过部分的面积.
扫过部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,五边形ABCDE中,∠A=140°,∠B=120°,∠E=90°,CP和DP分别是∠BCD、∠EDC的外角平分线,且相交于点P,则∠CPD=__________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
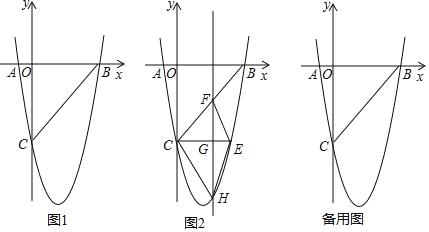
【题目】如图 1,在平面直角坐标系中,已知抛物线 y=ax2+bx﹣5 与 x 轴交于 A(﹣1,0),B(5, 0)两点,与 y 轴交于点 C.
(1)求抛物线的函数表达式;
(2)若点 D 是 y 轴上的一点,且以 B,C,D 为顶点的三角形与△ABC 相似,求点 D 的坐标;
(3)如图 2,CE∥x 轴与抛物线相交于点 E,点 H 是直线 CE 下方抛物线上的动点,过点 H且与 y 轴平行的直线与 BC,CE 分别相交于点 F,G,试探究当点 H 运动到何处时,四边形CHEF 的面积最大,求点 H 的坐标及最大面积;
(4)若点 K 为抛物线的顶点,点 M(4,m)是该抛物线上的一点,在 x 轴,y 轴上分别找点 P,Q,使四边形 PQKM 的周长最小,求出点 P,Q 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
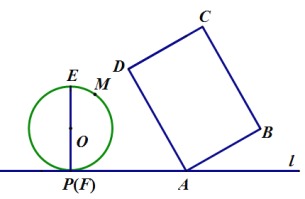
【题目】如图,在矩形![]() 中,
中,![]() ,点
,点![]() 在直线
在直线![]() 上,
上,![]() 与直线
与直线![]() 相交所得的锐角为
相交所得的锐角为![]() ,点
,点![]() 在直线
在直线![]() 上,
上,![]() ,垂足为点
,垂足为点![]() ,与点
,与点![]() 重合,
重合,![]() ,以
,以![]() 为直径,在
为直径,在![]() 的右侧作半圆
的右侧作半圆![]() ,点
,点![]() 是半圆
是半圆![]() 上任意一点.
上任意一点.
(1)发现:连接![]() ,则线段
,则线段![]() 的最大值为____________;
的最大值为____________;
(2)矩形![]() 保持不动,半圆
保持不动,半圆![]() 沿直线
沿直线![]() 向右平移,设平移距离为
向右平移,设平移距离为![]() .思考:点E落在边
.思考:点E落在边![]() 上时,求半圆
上时,求半圆![]() 与矩形
与矩形![]() 重合部分的面积
重合部分的面积![]() ;
;
(3)探究:在平移过程中,当半圆![]() 与矩形
与矩形![]() 的边相切时,直接写出
的边相切时,直接写出![]() 的值(参考数据:
的值(参考数据:![]() 结果保留根号)
结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:![]() ,
,![]() ,
,![]() ,将以上三个等式两边分别相加得:
,将以上三个等式两边分别相加得:![]() .
.
(1)观察发现
![]() _________;
_________;
![]() __________.
__________.
(2)初步应用
利用(1)的结论,解决下列问题:
①把![]() 拆成两个分子为1的正的真分数之差,即
拆成两个分子为1的正的真分数之差,即![]() __________;
__________;
②把![]() 拆成两个分子为1的正的真分数之和,即
拆成两个分子为1的正的真分数之和,即![]() __________.
__________.
(3)深入探究
定义“◆”是一种新的运算,若![]() ,
,![]() ,
,![]() ,则
,则![]() 计算的结果是_________.
计算的结果是_________.
(4)拓展延伸
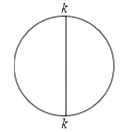
第一次用一条直径将圆周分成两个半圆(如图),在每个分点标上质数![]() ,记2个数的和为
,记2个数的和为![]() ,第二次将两个半圆都分成
,第二次将两个半圆都分成![]() 圆,在新产生的分点标相邻的已标的两个数的和的
圆,在新产生的分点标相邻的已标的两个数的和的![]() ,记4个数的和为
,记4个数的和为![]() ;第三次将四个
;第三次将四个![]() 圆分成
圆分成![]() 圆,在新产生的分点标相邻的已标的两个数的和的
圆,在新产生的分点标相邻的已标的两个数的和的![]() ,记8个数的和为
,记8个数的和为![]() ;第四次将八个
;第四次将八个![]() 圆分成
圆分成![]() 圆,在新产生的分点标相邻的已标的两个数的和的
圆,在新产生的分点标相邻的已标的两个数的和的![]() ,记16个数的和为
,记16个数的和为![]() ;……如此进行了
;……如此进行了![]() 次.
次.
①![]() _________(用含
_________(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
②![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
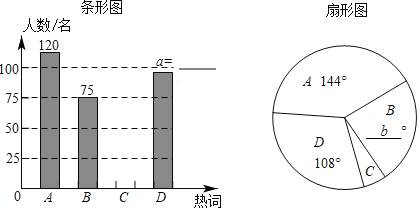
【题目】网络时代,新兴词汇层出不穷.为了解大众对网络词汇的理解,某兴趣小组举行了一个“我是路人甲”的调查活动:选取四个热词A:“硬核人生”,B:“好嗨哦”,C:“双击666”,D:“杠精时代”在街道上对流动人群进行了抽样调查,要求被调查的每位只能勾选一个最熟悉的热词,根据调查结果,该小组绘制了如下的两幅不完整的统计图,请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名路人.
(2)补全条形统计图;
(3)扇形图中的b= .
查看答案和解析>>
科目:初中数学 来源: 题型:
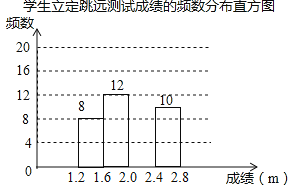
【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x<1.6 | a |
1.6≤x<2.0 | 12 |
2.0≤x<2.4 | b |
2.4≤x<2.8 | 10 |
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com