
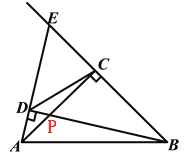
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=![]() ,点P是AC边上的一动点(点P不与端点A、C重合),过点A作AE⊥BP于D,交BC的延长线于点E.
,点P是AC边上的一动点(点P不与端点A、C重合),过点A作AE⊥BP于D,交BC的延长线于点E.
(1)求证:△ACE≌△BCP;
(2)在点P的移动过程中,若AD=DC,试求CP的长;
(3)试探索:在点P的移动过程中,∠ADC的大小是否保持不变?若保持不变,请求出∠ADC的大小;若有变化,请说明变化情况.
【答案】(1)见解析;(2)![]() ;(3)∠ADC的大小保持不变,为135°.
;(3)∠ADC的大小保持不变,为135°.
【解析】
(1)先证明![]() ,再根据AAS证明△ACE≌△BCP即可;
,再根据AAS证明△ACE≌△BCP即可;
(2)由勾股定理求出AB=2,由AD=DC得![]() 可证明
可证明![]() ,进而得
,进而得![]() ,由
,由![]() 得BE=AB=2,从而可求得答案;
得BE=AB=2,从而可求得答案;
(3)过点C分别作CF⊥BD于点F,CH⊥AE于点H,则![]() ,可证明△CFP≌△CHE,得∠EDC=
,可证明△CFP≌△CHE,得∠EDC=![]() ∠EDB=45°,故可求得∠ADC的大小保持不变,为135°.
∠EDB=45°,故可求得∠ADC的大小保持不变,为135°.
(1)证明:![]() ,即
,即![]() ,
,
![]()
![]()
![]()
![]()
在△ACE和△BCP中
![]()
![]()
![]()
![]() ;
;
(2)∵在![]() 中,
中,
![]()
![]()
![]()
![]()
![]()
![]() ,即
,即![]() ,
,
又![]()
![]() ,
,
![]() ,
,
![]() ;
;
(3)过点C分别作CF⊥BD于点F,CH⊥AE于点H,则![]() .
.
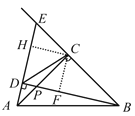
在△CFP与△CHE中,
∵ ∠CFP=∠CHE,
∠HEC=∠FPC,
CP=CE
∴△CFP≌△CHE,
∴CF=CH
∵CF⊥BD,CH⊥AE,
∴CD平分∠EDB,
∴∠EDC=![]() ∠EDB=45°,
∠EDB=45°,
∴∠ADC=180°-∠EDC=135°,
即∠ADC的大小保持不变,为135°.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,学校有一块长方形空地,它的长和宽的比是3:1,面积为363![]() .
.
(1)求该长方形的长和宽;
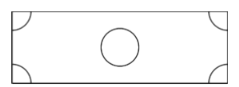
(2)如图所示,工人师傅要在这块空地上设计一个圆形区域和四个扇形区域进行绿化,其中四个扇形区域的半径与中间圆形区域半径相同,若绿化区域的总面积为![]() ,请你帮助工人师傅计算一下中间圆形区域的直径.
,请你帮助工人师傅计算一下中间圆形区域的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
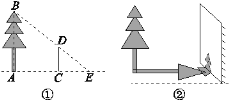
【题目】为了测量图①②中的树高,在同一时刻某人进行了如下操作:
图①:测得竹竿CD的长为0.8米,其影长CE为1米,树影AE长为2.4米.
图②:测得落在地面上的树的影长为2.8米,落在墙上的树影高1.2米.
请问图①和图②中的树高各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:以直线AB上一点O为端点作射线OM、ON,将一个直角三角形的直角顶点放在O处(∠COD=90°).
(1)如图1,直角三角板COD的边OD放在射线OB上,OM平分∠AOC,ON和OB重合,则∠MON=_°;
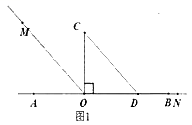
(2)直角三角板COD绕点O旋转到如图2的位置,OM平分∠AOC,ON平分∠BOD,求∠MON的度数。
(3)直角三角板COD绕点O旋转到如图3的位置,OM平分∠ AOC ,ON平分∠BOD,猜想∠MON的度数,并说明理由。
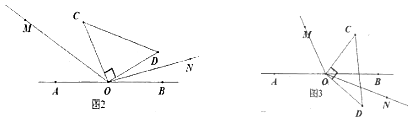
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(-4,![]() ),B(-1,2)是一次函数y=kx+b的图像与反比例函数
),B(-1,2)是一次函数y=kx+b的图像与反比例函数![]() (m≠0,m<0)的函数图像的两个交点,AC⊥x轴于点C,BD⊥y轴于点D
(m≠0,m<0)的函数图像的两个交点,AC⊥x轴于点C,BD⊥y轴于点D
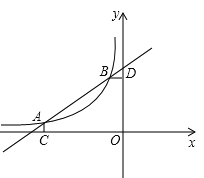
(1)根据函数图像直接回答问题:在第二象限内,当x取何值时,一次函数的值大于反比例函数的值?
(2)求一次函数的表达式及m的值;
(3)点P是线段AB上一点,连接PC,PD,若△PCA和△PBD的面积相等,求点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
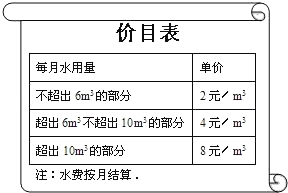
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表.
若某户居民1月份用水8m3,则应收水费:元
2×6+4×(8-6)=20
(1)若该户居民2月份用水12.5m3,则应收水费 元;
(2)若该户居民3、4月份共用水20m3(4月份用水量超过3月份),共交水费64元,则该户居民3,4月份各用水多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)学校组织学生参加综合实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如下表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
售价x(元/双) | 150 | 200 | 250 | 300 |
销售量y(双) | 40 | 30 | 24 | 20 |
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区的6名志愿者,在“十一”假期组织区内的未成年学生到公园秋游,公园的门票为每人40元,现有两种优惠方案,甲方案:志愿者免费,未成年学生按8折收费;乙方案:志愿者和未成年学生都按7折收费,若有![]() 名未成年学生.
名未成年学生.
(1)当![]() 时,甲方案需 元;乙方案需 元;
时,甲方案需 元;乙方案需 元;
(2)用含![]() 的式子表示两种方案各需多少元?
的式子表示两种方案各需多少元?
(3)当![]() 为何值时,甲、乙两种方案是一样的.
为何值时,甲、乙两种方案是一样的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O是等边三角形ABC的外接圆,P为劣弧BC上一点(点P与点B,C不重合).
(1)如果P是劣弧BC的中点,求证:PB+PC=PA;
(2)当点P在劣弧BC上移动时,(1)中的结论还成立吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com