
【题目】如图,在ABCD中,BD=2AB,AC与BD相交于点O,点E、F、G分别是OC、OB、AD的中点. 求证: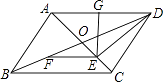
(1)DE⊥OC;
(2)EG=EF.
【答案】
(1)证明:∵四边形ABCD是平行四边形,AC与BD相交于点O,
∴BD=2OD,AB=CD,AD=BC.
∵BD=2AB,
∴OD=AB=CD.
∵点E是OC的中点,
∴DE⊥OC
(2)证明:∵DE⊥OC,点G是AD的中点,
∴EG= ![]() AD;
AD;
∵点E、F分别是OC、OB的中点.
∴EF= ![]() BC.
BC.
∵AD=BC,
∴EG=EF
【解析】(1)由四边形ABCD是平行四边形,AC与BD相交于点O,根据平行四边形的性质,即可得BD=2OD,AB=CD,AD=BC,又由BD=2AB,可得△ODC是等腰三角形,根据三线合一的性质,即可证得DE⊥OC;(2)由DE⊥OC,点G是AD的中点,利用直角三角形斜边上的中线等于斜边的一半,即可得EG= ![]() AD,又由三角形中位线的性质,求得EF=
AD,又由三角形中位线的性质,求得EF= ![]() BC,则可证得EG=EF.
BC,则可证得EG=EF.
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识,掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半,以及对平行四边形的性质的理解,了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( ) 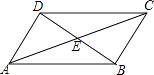
A.6
B.12
C.20
D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解业余射击队队员的射击成绩,对某次射击比赛中每一名队员的平均成绩(单位:环,环数为整数)进行了统计,分别绘制了如下统计表和频率分布直方图,请你根据统计表和频率分布直方图回答下列问题: 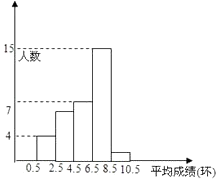
平均成绩 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
人数 | 0 | 1 | 3 | 3 | 4 | 6 | 1 | 0 |
(1)参加这次射击比赛的队员有多少名?
(2)这次射击比赛平均成绩的中位数落在频率分布直方图的哪个小组内?
(3)这次射击比赛平均成绩的众数落在频率分布直方图的哪个小组内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张长方形纸片与一张直角三角形纸片(∠EFG=90°)按如图所示的位置摆放,
使直角三角形纸片的一个顶点E恰好落在长方形纸片的一边AB上,已知∠BEF=21°,则
∠CMF= . 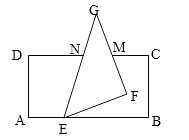
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点的位置如图所示,将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
利用网格点画图: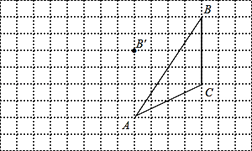
(1)画出△A′B′C′;
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)△A′B′C′的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设直线nx+(n+1)y= ![]() (n为自然数)与两坐标轴围成的三角形面积为Sn(n=1,2,…2014),则S1+S2+…+S2014的值为 .
(n为自然数)与两坐标轴围成的三角形面积为Sn(n=1,2,…2014),则S1+S2+…+S2014的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时15海里的速度航行,甲沿南偏西75°方向以每小时15![]() 海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.甲船追赶乙船的速度为多少海里/小时?
海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.甲船追赶乙船的速度为多少海里/小时?
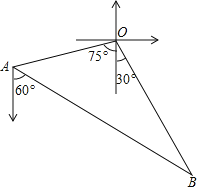
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com