
【题目】盒子里装有红球和白球共10个,它们除颜色外其他都相同,每次从盒子里摸出1个球,记下颜色后放回盒子里摇匀再摸.在摸球活动中得到下列表中部分数据.
摸球次数 | 出现红球的频数 | 出现红球的频率 | 摸球次数 | 出现红球的频数 | 出现红球的频率 |
50 | 17 | 34% | 350 | 103 | 29.4% |
100 | 32 | 32% | 400 | 123 | |
150 | 44 | 29.3% | 450 | 136 | 30.2% |
200 | 64 | 32% | 500 | 148 | 29.6% |
250 | 78 | 31.2% | 550 | 167 | |
300 | 32% | 600 | 181 | 30.2% |
(1)请将表中数据补充完整.
(2)画出出现红球的频率的折线统计图.
(3)观察所画折线统计图,你发现了什么?
(4)你认为盒子里哪种颜色的球多?
(5)如果从盒子里任意摸出一球,你认为摸到白球的概率有多大?
【答案】(1) 96;30.8%;30.4%;(2)详见解析;(3)观察折线统计图可以发现:随着摸球次数的增多,出现红球的频率在30%上下浮动.(4)由(3)可以估计盒子里白球的个数比红球多.(5)70%.
【解析】试题分析:(1)利用频数=频率×摸球次数计算数据即可;
(2)根据表格提供的数据作出条形统计图即可;
(3)通过观察统计图找到其频率逐渐稳定到哪个常数附近即可;
(4)根据频率的大小进行比较即可;
(5)用1减去摸到红球的概率就是摸到白球的概率.
试题解析:(1)表中依次填为:96;30.8%;30.4%从左往右,从上往下.
(2)如图:
 .
.
(3)观察折线统计图可以发现:随着摸球次数的增多,出现红球的频率在30%上下浮动.
(4)由(3)可以估计盒子里白球的个数比红球多.
(5)如果从盒子里任意摸出一球,摸到白球的概率是
1-30%=70%.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点E为边AB上任意一点,点D在边CB的延长线上,且ED=EC.

(1)当点E为AB的中点时(如图1),则有AE DB(填“>”“<”或“=”);
(2)猜想AE与DB的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题7分)一个不透明的口袋里装有分别标有汉字“灵”、“秀”、“黄”、“冈”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字刚好是“黄”的概率为多少?
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图的方法,求出甲取出的两个球上的汉字恰能组成“灵秀”或“黄冈”(汉字不分先后顺序)的概率P1;
(3)乙从中任取一球,记下汉字后再放回袋中,然后再从中任取一球,记乙取出的两个球上的汉字恰能组成“灵秀”或“黄冈”(汉字不分先后顺序)的概率为P2,请直接写出P2的值,并比较P1,P2的大小.(2+3+2=7)
查看答案和解析>>
科目:初中数学 来源: 题型:
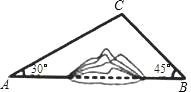
【题目】如图,A,B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A﹣C﹣B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10km,∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1km)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划2016年在甲、乙两个电视台播放总时长为300分钟的广告,已知甲、乙两电视台的广告收费标准分别为500元/分钟和200元/分钟,该公司的广告总费用为9万元.预计甲、乙两个电视台播放该公司的广告能给该公司分别带来0.3万元/分钟和0.2万元/分钟的收益,该公司在甲、乙两个电视台播放广告的时长应分别为多少分钟?预计甲、乙两电视台2016年为此公司所播放的广告将给该公司带来多少万元的总收益?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商人制成了一个如图所示的转盘,取名为“开心大转盘”,游戏规定:参与者自由转动转盘,转盘停止后,若指针指向字母“A”,则收费2元,若指针指向字母“B”,则奖励3元;若指针指向字母“C”,则奖励1元.一天,前来寻开心的人转动转盘80次,你认为该商人是盈利的可能性大还是亏损的可能性大?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个质地均匀的正12面体,12个面上分别写有1~12这12个整数(每个面只有一个整数且互不相同).投掷这个正12面体一次,记事件A为“向上一面的数字是2或3的整数倍”,记事件B为“向上一面的数字是3的整数倍”,请你判断等式P(A)=![]() +P(B)是否成立,并说明理由.
+P(B)是否成立,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为( )
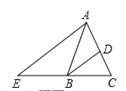
A. 40° B. 45° C. 60° D. 70°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com