
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:解答题
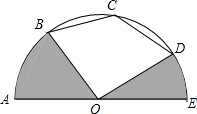 如图,半圆O的直径AE=4,点B、C、D均在半圆上,若AB=BC,CD=DE,连接OB、OD,
如图,半圆O的直径AE=4,点B、C、D均在半圆上,若AB=BC,CD=DE,连接OB、OD,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 飞机起飞前,对其零部件进行检查 | B. | 调查一个条河流的水污染情况 | ||
| C. | 调查一批新型节能灯的使用寿命 | D. | 调查湖南省七年级学生的身高情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,等边△ABC中,D、E分别为BC、AC上一点,且BD=CE.
如图,等边△ABC中,D、E分别为BC、AC上一点,且BD=CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com