
 如图,AO⊥BC,DO⊥OE.求证:∠AOD=∠COE,∠BOD=∠AOE.
如图,AO⊥BC,DO⊥OE.求证:∠AOD=∠COE,∠BOD=∠AOE. 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
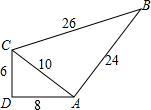 一个零件的形状如图所示,按规定这个零件中∠BAC和∠ADC都应为直角,工人师傅量的零件各边尺寸:AD=8,AC=10,CD=6,AB=24,BC=26,请你判断这个零件是否符合要求,并说明理由.
一个零件的形状如图所示,按规定这个零件中∠BAC和∠ADC都应为直角,工人师傅量的零件各边尺寸:AD=8,AC=10,CD=6,AB=24,BC=26,请你判断这个零件是否符合要求,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
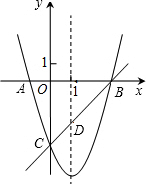 如图,已知抛物线y=x2+bx+c与x轴相交于A,B两点(A点在B点的左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
如图,已知抛物线y=x2+bx+c与x轴相交于A,B两点(A点在B点的左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com