
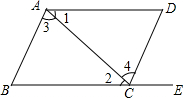
 如图,给出下列条件:
如图,给出下列条件:| A. | ①② | B. | ②④ | C. | ②③ | D. | ②③④ |
分析 根据平行线的判定条件,逐一判断,排除错误答案.
解答 解:①∵∠1=∠2,∴AD∥BC,故此选项错误;
②∵∠3=∠4,∴AB∥DC,(内错角相等,两直线平行),故此选项正确;
③∵AD∥BC,∴∠B+∠BAD=180°,∵∠D=∠B,∴∠D+∠BAD=180°,由同旁内角互补,两直线平行可得AB∥DC,故此选项正确;
④∵AD∥BC,∴∠B+∠BAD=180°,∵∠BAD=∠BCD,∴∠B+∠BCD=180°,由同旁内角互补,两直线平行可得AB∥DC,故此选项正确;
故能推出AB∥DC的条件为:②③④.
故选D.
点评 此题考查了平行线的判定与性质,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 2或-5 | B. | -2或5 | C. | 2或5 | D. | -2或-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<0 | |
| B. | a>0 | |
| C. | 方程ax2+bx+c=0必有一根x0满足x1<x0<x2 | |
| D. | y1<y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛一枚硬币,正面朝上 | |
| B. | 黑暗中从5把不同的钥匙中随意摸出一把,用它打开了门 | |
| C. | 打开电视机,任选一个频道,屏幕上正在播放新闻联播 | |
| D. | 4个人分成3组,其中一组必有2人 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com