

���� ��1������A����������A����ռ�İٷֱȣ��ɵó�����������
��2�����ݳ����������ȥA����B���������ɵ�C������������C���������ɵô𰸣�
��3������Բ�ܽdz���C����ռ�İٷֱȣ��ɵô𰸣�
��4������ѧУ����������A����B����ռ�ٷֱȵĺͣ��ɵô𰸣�
��� �⣺��1���˴γ��������У���������50��25%=200��ѧ����
�ʴ�Ϊ��200��
��2��C������Ϊ200-50-120=30���ˣ���
����ͳ��ͼ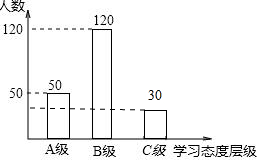 ��
��
��3��C����ռԲ�ĽǶ�����360�����1-25%-60%��=360���15%=54��
��4���������Լ��8000����25%+60%��=6800���ˣ���
���� ���⿼��������ͳ��ͼ���۲�ͳ��ͼ�����Ч��Ϣ�ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У���P��Բ�������ǣ�3��a����a��3�����뾶Ϊ3������y=x��ͼ��P�صõ���AB�ij�Ϊ4$\sqrt{2}$����a��ֵ��3+$\sqrt{2}$��
��ͼ����ƽ��ֱ������ϵ�У���P��Բ�������ǣ�3��a����a��3�����뾶Ϊ3������y=x��ͼ��P�صõ���AB�ij�Ϊ4$\sqrt{2}$����a��ֵ��3+$\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4$\sqrt{3}$ | B�� | $\sqrt{3}$ | C�� | 2$\sqrt{3}$ | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
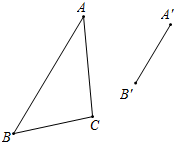 ��ͼ����֪��ABC�͡�A��B��C����λ�Ʊ�Ϊ2��λ�������Σ���AB�Ķ�Ӧ����A��B�䣬���ó߹���ͼ������A��B��C�䲹���������ɲ�д��������������ͼ�ۼ�����
��ͼ����֪��ABC�͡�A��B��C����λ�Ʊ�Ϊ2��λ�������Σ���AB�Ķ�Ӧ����A��B�䣬���ó߹���ͼ������A��B��C�䲹���������ɲ�д��������������ͼ�ۼ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
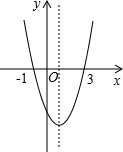 ���κ���y=ax2+bx+c��ͼ����ͼ��ʾ����������˵������bc��0���ڷ���ax2+bx+c=0�ĸ�Ϊx1=-1��x2=3����4a-2b+c��0���ܵ�x��0ʱ��y��xֵ����������ݵ�y��0ʱ��-1��x��3��������ȷ�ĸ����ǣ�������
���κ���y=ax2+bx+c��ͼ����ͼ��ʾ����������˵������bc��0���ڷ���ax2+bx+c=0�ĸ�Ϊx1=-1��x2=3����4a-2b+c��0���ܵ�x��0ʱ��y��xֵ����������ݵ�y��0ʱ��-1��x��3��������ȷ�ĸ����ǣ�������| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com