
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() 于
于![]() 点,若
点,若![]() ,则
,则![]() 的半径为( )
的半径为( )
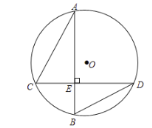
A.![]() B.5C.
B.5C.![]() D.
D.![]()
【答案】C
【解析】
由AB⊥CD,∠CDB=30°,在Rt△BDE中可以先求出EB;由同弧所对圆周角相等,则∠CAE=30°,在Rt△ACE中由AC可以求出CE;连接BC,由勾股定理可求出BC;连接OC,OB可知∠COB=2∠CDB=60°,此时△COB为等边三角形,半径长即为CB的长.
解:如下图所示:连接OC、OB、CB,
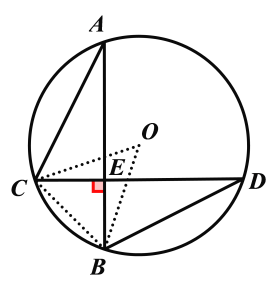
∵AB⊥CD,∠CDB=30°,BD=4,
∴BE=![]() BD=2,
BD=2,
由同弧所对圆周角相等知:∠CAB=∠CDB=30°,
由AC=6,可知CE=3,
在Rt△CEB中,由勾股定理可知:![]()
由同弧所对圆周角等于圆心角的一半知:
∠COB=2∠CDB=60°,且OC=OB,
此时△COB为等边三角形,
∴半径即为![]() .
.
故答案为:C.


科目:初中数学 来源: 题型:
【题目】如图1,![]() 内接于
内接于![]() ,点
,点![]() 为
为![]() 中点,点
中点,点![]() 在
在![]() 上,连接
上,连接![]() 点
点![]() 是
是![]() 的中点,连结
的中点,连结![]() .
.
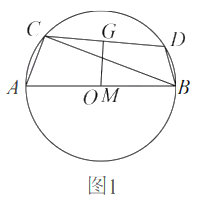
(1)求证:![]() ;
;
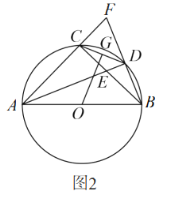
(2)如图2,若![]() 平分
平分![]() 与
与![]() 交于点
交于点![]() 延长
延长![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() 求证:
求证:![]() ;
;
(3)在(2)的条件下,若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=6,E为AD上一点,将△BAE绕点B顺时针旋转得到△BA′E′,当点A′,E′分别落在BD,CD上时,则DE的长为_____.
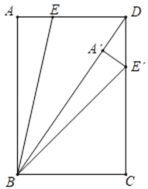
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇乘坐一艘游船出海游玩,游船上的雷达扫描探测得到的结果如图所示,每相邻两个圆之间距离是1km (最小圆的半径是1km ),下列关于小艇 A , B 的位置描述,正确的是( )

A.小艇 A 在游船的北偏东60°方向上,且与游船的距离是3km
B.游船在小艇 A 的南偏西60°方向上,且与小艇 A 的距离是3km
C.小艇 B 在游船的北偏西30°方向上,且与游船的距离是 2km
D.游船在小艇 B 的南偏东60°方向上,且与小艇 B 的距离是 2km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形![]() 的边长为4,一个以点
的边长为4,一个以点![]() 为顶点的
为顶点的![]() 角绕点
角绕点![]() 旋转,角的两边分别与边
旋转,角的两边分别与边![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() ,设
,设![]() .
.
(1)如图1,当![]() 被对角线
被对角线![]() 平分时,求
平分时,求![]() 的值;
的值;
(2)求证:![]() 与
与![]() 相似;
相似;
(3)当![]() 的外心在其边上时,求
的外心在其边上时,求![]() 的值.
的值.
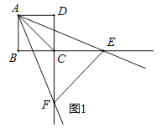
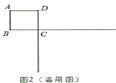

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“西成高铁”的开通,对于加强关中一天水经济区与成渝经济区的交流合作,促进区域经济发展和提高人民出行质量,具有十分重要的意义.成都某单位计划组织优秀员工利用周末乘坐“西成高铁”到西安观光旅游,计划游览著名景点“大唐芙蓉园”,该景区团体票价格设置如下:
人数/人 | 10人以内(含10人) | 超过10人但不超过30人的部分 | 超过30人的部分 |
单价(元/张) | 120 | 108 | 96 |
(1)求团体票价![]() 与游览人数
与游览人数![]() 之间的函数关系式;
之间的函数关系式;
(2)若该单位购买团体票共花费3456元,且所有人都购买了门票,那么该单位共有多少人游览了“大唐芙蓉园”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组的同学在研究函数![]() 的图象时,先对函数
的图象时,先对函数![]() 的图象进行了如下探索.
的图象进行了如下探索.
![]() ①列表:列出
①列表:列出![]() 与
与![]() 的几组对应值如下:
的几组对应值如下:
| ··· |
|
|
|
|
|
|
|
|
|
| ··· |
| ··· |
|
|
|
|
|
|
|
|
|
| ··· |
②描点:根据表中数据描点如图所示;
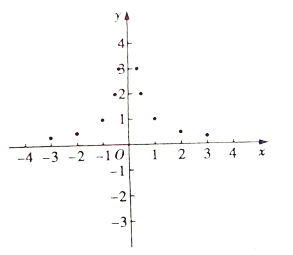
③连线:请在图中画出函数![]() 的图象;
的图象;
④观察图象,写出两条关于该函数的性质.
![]() 根据以上探究结果,完成下列问题:
根据以上探究结果,完成下列问题:
①函数![]() 中,自变量
中,自变量![]() 的取值范围为 ;
的取值范围为 ;
②函数![]() 的图象可由函数
的图象可由函数![]() 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
③写出两条关于函数![]() 的性质;
的性质;
④直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,
,![]() 在正方形外,
在正方形外,![]() ,过
,过![]() 作
作![]() 于
于![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,则下列结论正确的是( )
,则下列结论正确的是( )

①![]() ;②
;②![]() ;③
;③![]() ;
;
④若![]() ,则
,则![]()
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有三个小球,上面分别标有数字3、4、5,这些小球除数字不同外其余均相同.
(1)从口袋中随机摸出一个小球,小球上的数字是偶数的概率是______.
(2)从口袋中随机摸出一个小球,记下数字后放回,再随机摸出一个小球,记下数字,请用画树状图(或列表)的方法,求两次摸出的小球上的数字都是奇数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com