
 (1)cos245°+tan30°sin60°;
(1)cos245°+tan30°sin60°;分析 (1)根据特殊角的锐角三角函数值计算即可;
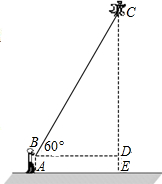
(2)根据直角三角形的性质求出BD的长,根据勾股定理求出CD的长,根据CE=CD+DE求出答案即可.
解答 解:(1)原式=$\frac{1}{2}$+$\frac{\sqrt{3}}{3}$×$\frac{\sqrt{3}}{2}$,
=$\frac{1}{2}$+$\frac{1}{2}$,
=1;
(2)解:∵∠CDB=90°,∠CBD=60°,
∴∠C=30°,
∴BD=$\frac{1}{2}$BC=10米,
∴CD=10$\sqrt{3}$米,
∴CE=CD+DE=(10$\sqrt{3}$+1.5)≈18.8米,
答:此时风筝离地面的高度CE约为18.8米.
点评 本题考查的是勾股定理的应用,解题关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.


科目:初中数学 来源: 题型:选择题
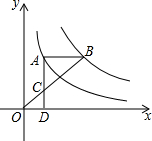 如图,点A在双曲线y=$\frac{3}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
如图,点A在双曲线y=$\frac{3}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )| A. | 6 | B. | 9 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3⊥OP2且P2P3=1,得OP3=2,;…依次法继续作下去,则OP2015长为( )
如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3⊥OP2且P2P3=1,得OP3=2,;…依次法继续作下去,则OP2015长为( )| A. | 2015 | B. | 2016 | C. | $\sqrt{2015}$ | D. | $\sqrt{2016}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知依次函数y=x+1.
已知依次函数y=x+1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
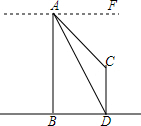 随着科技的发展,无人机现在已经有了更加广泛的应用,如图所示,一测绘机利用无人机测量某电视塔的高度.某一时刻,无人机的高度AB=500米,无人机此时在A处测得电视塔顶端C和底端D的俯角分别为45°和60°,求电视塔的高度.
随着科技的发展,无人机现在已经有了更加广泛的应用,如图所示,一测绘机利用无人机测量某电视塔的高度.某一时刻,无人机的高度AB=500米,无人机此时在A处测得电视塔顶端C和底端D的俯角分别为45°和60°,求电视塔的高度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
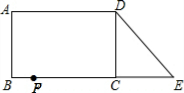 已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时.△ABP和△DCE全等.
已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时.△ABP和△DCE全等.| A. | 1 | B. | 1或3 | C. | 1或7 | D. | 3或7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com