
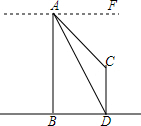
 随着科技的发展,无人机现在已经有了更加广泛的应用,如图所示,一测绘机利用无人机测量某电视塔的高度.某一时刻,无人机的高度AB=500米,无人机此时在A处测得电视塔顶端C和底端D的俯角分别为45°和60°,求电视塔的高度.
随着科技的发展,无人机现在已经有了更加广泛的应用,如图所示,一测绘机利用无人机测量某电视塔的高度.某一时刻,无人机的高度AB=500米,无人机此时在A处测得电视塔顶端C和底端D的俯角分别为45°和60°,求电视塔的高度. 分析 延长DC交AF于F,易得四边形ABCF是矩形,根据三角函数关系和BD的长度可得出答案.
解答 解:延长DC交AF于F,则四边形ABCF是矩形,
∴AF=BD,AB=DF,
由题意得:∠FAC=45°,∠FAD=60°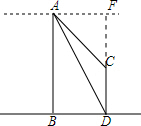 ,
,
∴∠BAD=30°,∠ACF=45°,
∴AF=CF,
∵AB=500米,
∴BD=AF=FC=$\frac{500\sqrt{3}}{3}$米,
∴CD=DF-FC=AB-FC=500-$\frac{500\sqrt{3}}{3}$=$\frac{1500-500\sqrt{3}}{3}$米,
即电视塔的高度为$\frac{1500-500\sqrt{3}}{3}$米.
点评 本题考查解直角三角形的应用,关键在于根据题意画出图形,然后根据三角函数关系求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)cos245°+tan30°sin60°;
(1)cos245°+tan30°sin60°;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
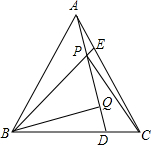 如图,在等边三角形△ABC中,AE=CD,AD、BE交于P点,BQ⊥AD于Q,
如图,在等边三角形△ABC中,AE=CD,AD、BE交于P点,BQ⊥AD于Q,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com