
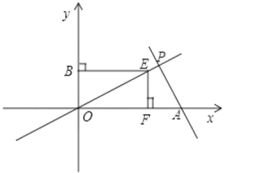
【题目】已知如图,直线y=﹣![]() x+4
x+4![]() 与x轴相交于点A,与直线y=
与x轴相交于点A,与直线y= ![]() x相交于点P.
x相交于点P.
(1)求点P的坐标;
(2)动点E从原点O出发,沿着O→P→A的路线向点A匀速运动(E不与点O、A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时, F的坐标为(a,0),矩形EBOF与△OPA重叠部分的面积为S.直接写出: S与a之间的函数关系式
(3)若点M在直线OP上,在平面内是否存在一点Q,使以A,P,M,Q为顶点的四边形为矩形且满足矩形两边AP:PM之比为1:![]() 若存在直接写出Q点坐标。若不存在请说明理由。
若存在直接写出Q点坐标。若不存在请说明理由。
【答案】(1)![]() ; (2)
; (2)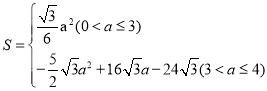 ;(3)
;(3)![]()
【解析】
(1)联立两直线解析式,求出交点P坐标即可;
(2)由F坐标确定出OF的长,得到E的横坐标为a,代入直线OP解析式表示出E纵坐标,即为EF的长,分两种情况考虑:当![]() 时,矩形EBOF与三角形OPA重叠部分为直角三角形OEF,表示出三角形OEF面积S与a的函数关系式;当
时,矩形EBOF与三角形OPA重叠部分为直角三角形OEF,表示出三角形OEF面积S与a的函数关系式;当![]() 时,重合部分为直角梯形面积,求出S与a函数关系式.
时,重合部分为直角梯形面积,求出S与a函数关系式.
(3)根据(1)所求,先求得A点坐标,再确定AP和PM的长度分别是2和2![]() ,又由OP=2
,又由OP=2![]() ,得到P怎么平移会得到M,按同样的方法平移A即可得到Q.
,得到P怎么平移会得到M,按同样的方法平移A即可得到Q.
解:(1)联立得: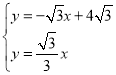 ,解得:
,解得: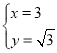 ;
;
∴P的坐标为![]() ;
;
(2)分两种情况考虑:
当![]() 时,由F坐标为(a,0),得到OF=a,
时,由F坐标为(a,0),得到OF=a,
把E横坐标为a,代入![]() 得:
得:![]() 即
即![]()
此时![]()
当![]() 时,重合的面积就是梯形面积,
时,重合的面积就是梯形面积,
F点的横坐标为a,所以E点纵坐标为![]()
M点横坐标为:-3a+12,
∴![]()
所以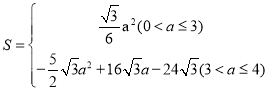 ;
;
(3)令![]() 中的y=0,解得:x=4,则A的坐标为(4,0)
中的y=0,解得:x=4,则A的坐标为(4,0)
则AP=![]() ,则PM=2
,则PM=2![]()
又∵OP=![]()
∴点P向左平移3个单位在向下平移![]() 可以得到M1
可以得到M1
点P向右平移3个单位在向上平移![]() 可以得到M2
可以得到M2
∴A向左平移3个单位在向下平移![]() 可以得到 Q1(1,-
可以得到 Q1(1,-![]() )
)
A向右平移3个单位在向上平移![]() 可以得到 Q1(7,
可以得到 Q1(7,![]() )
)
所以,存在Q点,且坐标是![]()


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】某公园要修建一个截面抛物线形的拱门,其最大高度为4.5m,宽度OP为6米,现以地面(OP所在的直线)为x轴建立平面直角坐标系(如图1所示)
(1)求这条抛物线的函数表达式;
(2)如图所示,公园想在抛物线拱门距地面3米处钉两个钉子以便拉一条横幅,请计算该横幅的宽度为多少米?
(3)为修建该拱门,施工队需搭建一个矩形“支架“ABCD(由四根木杆AB﹣BC﹣CD﹣DA组成),使B,C两点在抛物线上.A,D两点在地面OP上(如图2所示),请你帮施工队计算一下最多需要准备多少米该种木杆?
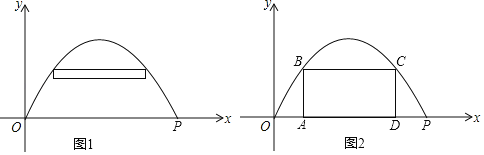
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.
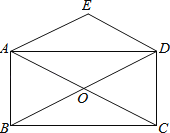
(1)求证:四边形AODE是菱形;
(2)若将题设中“矩形ABCD”这一条件改为“菱形ABCD”,其余条件不变,则四边形AODE的形状是什么?不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】河西中学九年级共有9个班,300名学生,学校要对该年级学生数学学科学业水平测试成绩进行抽样分析,请按要求回答下列问题:
收集数据
(1)若从所有成绩中抽取一个容量为36的样本,以下抽样方法中最合理的是 .
①在九年级学生中随机抽取36名学生的成绩;
②按男、女各随机抽取18名学生的成绩;
③按班级在每个班各随机抽取4名学生的成绩.
整理数据
(2)将抽取的36名学生的成绩进行分组,绘制频数分布表和成绩分布扇形统计图如下.请根据图表中数据填空:
①C类和D类部分的圆心角度数分别为 °、 °;
②估计九年级A、B类学生一共有 名.
成绩(单位:分) | 频数 | 频率 |
A类(80~100) | 18 |
|
B类(60~79) | 9 |
|
C类(40~59) | 6 |
|
D类(0~39) | 3 |
|
分析数据
(3)教育主管部门为了解学校教学情况,将河西、复兴两所中学的抽样数据进行对比,得下表:
学校 | 平均数(分) | 极差(分) | 方差 | A、B类的频率和 |
河西中学 | 71 | 52 | 432 | 0.75 |
复兴中学 | 71 | 80 | 497 | 0.82 |
你认为哪所学校本次测试成绩较好,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
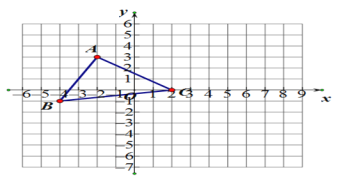
【题目】在平面直角坐标系中,△ABC的顶点坐标是A(﹣2,3),B(﹣4,﹣1), C(2,0).点P(m,n)为△ABC内一点,平移△ABC得到△A1B1C1 ,使点P(m,n)移到P(m+6,n+1)处.
(1)画出△A1B1C1
(2)将△ABC绕坐标点C逆时针旋转90°得到△A2B2C,画出△A2B2C;
(3)在(2)的条件下求BC扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】儿童节前,某玩具商店根据市场调查,用3000元购进一批儿童玩具,上市后很快脱销,接着又用5400元购进第二批这种玩具,所购数量是第一批数量的1.5倍,但每套进价多了10元.
(1)求第一批玩具每套的进价是多少元?
(2)如果这两批玩具每套售价相同,且全部售完后总利润不低于25%,那么每套玩具售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,直线y=
x2+bx+c与x轴交于A、B两点,直线y=![]() x+
x+![]() 经过点A,与抛物线的另一个交点为点C(3,m),线段PQ在线段AB上移动,PQ=1,分别过点P、Q作x轴的垂线,交抛物线于E、F,交直线于D、G.
经过点A,与抛物线的另一个交点为点C(3,m),线段PQ在线段AB上移动,PQ=1,分别过点P、Q作x轴的垂线,交抛物线于E、F,交直线于D、G.
(1)求抛物线的解析式;
(2)设四边形DEFG的面积为S,求S的最大值;
(3)在线段PQ的移动过程中,以D,E,F,G为顶点的四边形是平行四边形时,求点P的坐标.
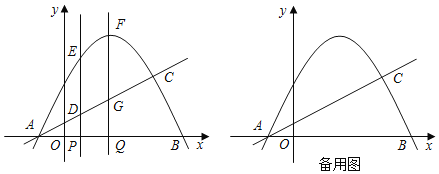
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD中,AB=5,点E为BC边上一动点,连接AE,以AE为边,在线段AE右侧作正方形![]() ,连接CF、DF.设
,连接CF、DF.设![]() .(当点E与点B重合时,x的值为0),
.(当点E与点B重合时,x的值为0),![]() .小明根据学习函数的经验,对函数
.小明根据学习函数的经验,对函数![]() 随自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整:
随自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整:
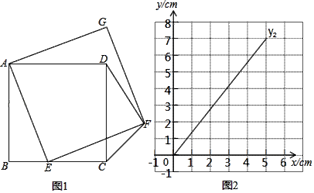
(1)通过取点、画图、测量、观察、计算,得到了x与y1、y2的几组对应值;
x | 0 | 1 | 2 | 3 | 4 | 5 |
| 5.00 | 4.12 | 3.61 | 4.12 | 5.00 | |
| 0 | 1.41 | 2.83 | 4.24 | 5.65 | 7.07 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点![]() ,并画出函数y1,y2的图象;
,并画出函数y1,y2的图象;
(3)结合函数图象2,解决问题:当△CDF为等腰三角形时,BE的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
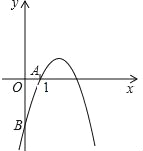
【题目】如图,抛物线y=﹣x2+5x+n经过点A(1,0),与y轴交于点B.
(1)求抛物线的解析式;
(2)P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求P点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com