
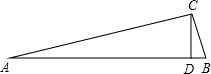
 已知:如图,在Rt△ABC中,∠C=90°,∠B=5∠A,CD⊥AB,垂足为D,求证:AB=4CD.(提示.作斜边AB上的中线CM)
已知:如图,在Rt△ABC中,∠C=90°,∠B=5∠A,CD⊥AB,垂足为D,求证:AB=4CD.(提示.作斜边AB上的中线CM) 分析 作斜边AB上的中线CM,由∠C=90°,∠B=5∠A,根据三角形的内角和得到∠A+∠B=∠A+5∠A=6∠A=90°,求得∠A=15°,根据直角三角形的性质得到AM=CM,由等腰三角形的性质得到∠A=∠ACM=15°,根据外角的性质得到∠CMD=30°,于是得到CM=2CD,依此得到结论.
解答 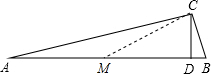 证明:作斜边AB上的中线CM,
证明:作斜边AB上的中线CM,
∵∠C=90°,∠B=5∠A,
∴∠A+∠B=∠A+5∠A=6∠A=90°,
∴∠A=15°,
∵CM是在Rt△ABC斜边AB上的中线,
∴AM=CM,
∴∠A=∠ACM=15°,
∴∠CMD=30°,
∵CD⊥AB,
∴∠CDM=90°,
∴CM=2CD,
∴AB=2CM=4CD.
点评 本题考查了含30°角的直角三角形的性质,等腰三角形的判定和性质,正确的作出辅助线是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
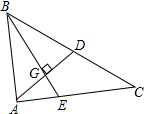 我们知道,三角形的三条中线一定会交于一点,这一点就叫做三角形的重心.重心有很多“美妙”的性质.如关于线段比、面积比就有一些“漂亮”的结论,利用这些性质可以解决三角形的若干问题.请你利用重心的性质解决如下问题:
我们知道,三角形的三条中线一定会交于一点,这一点就叫做三角形的重心.重心有很多“美妙”的性质.如关于线段比、面积比就有一些“漂亮”的结论,利用这些性质可以解决三角形的若干问题.请你利用重心的性质解决如下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com