
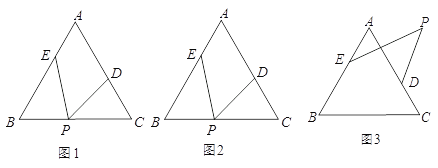
【题目】△ABC中,∠A=60°,点D、E分别是△ABC边AC、AB上的点(不与A、B、C重合),点P是一动点,令∠PDC=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在边BC上,如图l,且∠α=50°,则∠1+∠2= °.
(2)若点P在边BC上运动,如图2,试判断∠α、∠1、∠2之间的关系,并证明.
(3)直接写出:若点P运动到△ABC形外,如图3,则∠α、∠l、∠2之间的关系为 .
【答案】(1)110°;(2)猜想:∠1+∠2=60°+∠![]() 证明见解析;(3)∠2-∠1+∠
证明见解析;(3)∠2-∠1+∠![]() =60°
=60°
【解析】试题分析:(1)连接PA,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠1=∠PAD+∠APD,∠2=∠PAE+∠APE,再表示出∠1+∠2即可;(2)利用(1)中所求得出答案即可;(3)利用三角形内角和定理以及邻补角的性质可得出.
试题解析:
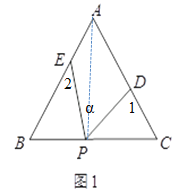
(1)如图,连接PC,
∵∠1=∠PAD+∠APD,∠2=∠PAE+∠APE,
∴∠1+∠2=∠PAD+∠APD+∠PAE+∠APE=∠DPE+∠A,
∵∠DPE=∠α=50°,∠A=60°,
∴∠1+∠2=50°+60°=110°
故答案为:110°;
(2)如图:连接PA,
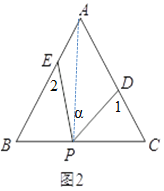
∵∠1=∠PAD+∠APD,∠2=∠PAE+∠APE
∴∠1+∠2=∠PAD+∠APD+∠PAE+∠APE=∠DPE+∠A,
∵∠A=60°,∠DPE=∠α,
∴∠1+∠2=60°+∠α;
故答案为:∠1+∠2=60°+∠α;
(3)如图,
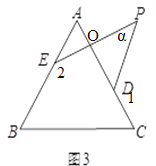
∵∠2=∠A+∠AOE,
∠1=∠α+∠POD;
∠AOE=∠POD
∴∠1∠2=∠A-∠α
即∠1∠2+∠α==60°


科目:初中数学 来源: 题型:
【题目】将多项式3x2y-xy2+x3y3-x4y4-1按字母x的降幂排列,则下列各式正确的是( )
A. -1-xy2+3x2y+x3y3-x4y4
B. -x4y4+x3y3+3x2y-xy2-1
C. -x4y4+x3y3-xy2+3x2y-1
D. -1+3x2y-xy2+x3y3-x4y4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是![]() ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
A. 2,![]() B. 2,1 C. 4,
B. 2,1 C. 4,![]() D. 4,3
D. 4,3
查看答案和解析>>
科目:初中数学 来源: 题型:
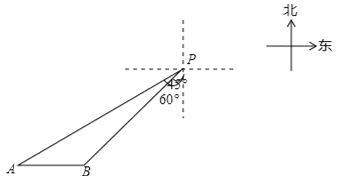
【题目】一艘轮船位于灯塔P南偏西60°方向,距离灯塔20海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:![]() ≈1.732,结果精确到0.1)?
≈1.732,结果精确到0.1)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的表格是李刚同学一学期数学成绩的记录,根据表格提供的信息回答下面的问题
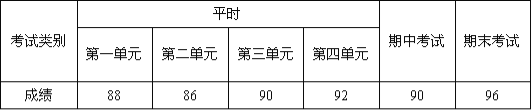
(1)李刚同学6次成绩的极差是 .
(2)李刚同学6次成绩的中位数是 .
(3)李刚同学平时成绩的平均数是 .
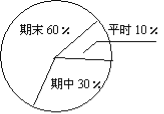
(4)如果用右图的权重给李刚打分,他应该得多少分?(满分100分,写出解题过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com