
【题目】如图,在△ABC中,∠ABC=90°,AB=12,BC=5,若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )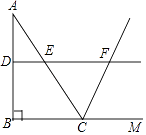
A.6
B.7
C.8
D.9
【答案】D
【解析】解:∵∠ABC=90°,AB=12,BC=5,
∴AC= ![]() =13,
=13,
∵DE是△ABC的中位线,
∴DE= ![]() BC=2.5,DE∥BC,EC=
BC=2.5,DE∥BC,EC= ![]() AC=6.5,
AC=6.5,
∵CF是△ABC的外角∠ACM的平分线,
∴∠ECF=∠MCF,
∵DE∥BC,
∴∠EFC=∠MCF,
∴∠ECF=∠EFC,
∴EF=EC=6.5,
∴DF=DE+EF=9,
所以答案是:D.
【考点精析】根据题目的已知条件,利用三角形的外角和三角形中位线定理的相关知识可以得到问题的答案,需要掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数 ![]() 与方差s2:
与方差s2:
甲 | 乙 | 丙 | 丁 | |
平均数 | 561 | 560 | 561 | 560 |
方差s2(cm2) | 3.5 | 3.5 | 15.5 | 16.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A.甲
B.乙
C.丙
D.丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.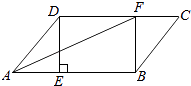
(1)求证:四边形BFDE是矩形;
(2)若AD=DF,求证:AF平分∠BAD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是AD上的一个动点,连接BE,作点A关于BE的对称点F,且点F落在矩形ABCD的内部,连接AF,BF,EF,过点F作GF⊥AF交AD于点G,设![]() .
.
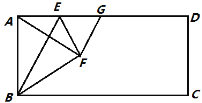
(1)求证:AE=GE;
(2)当点F落在AC上时,用含n的代数式表示![]() 的值;
的值;
(3)若AD=4AB,且以点F,C,G为顶点的三角形是直角三角形,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是矩形ABCD的边AD上的一动点,AB=6,BC=8,则点P到矩形的两条对角线AC和BD的距离之和是( )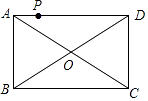
A.4.8
B.5
C.6
D.7.2
查看答案和解析>>
科目:初中数学 来源: 题型:
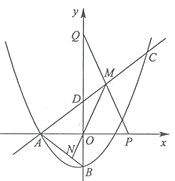
【题目】如图,抛物线![]() 与
与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连结
,连结![]() ,点
,点![]() 在抛物线上,直线
在抛物线上,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值及直线
的值及直线![]() 的函数表达式;
的函数表达式;
(2)点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在
在![]() 轴正半轴上,连结
轴正半轴上,连结![]() 与直线
与直线![]() 交于点
交于点![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,若
,若![]() 为
为![]() 的中点.
的中点.
①求证:![]() ;
;
②设点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 的长(用含
的长(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com