
【题目】如图,∠AOC与∠BOC互余,OD平分∠BOC,∠AOE=2∠EOC.
(1)若∠AOD=75°,求∠AOE的度数.
(2)若∠DOE=36°,求∠EOC的度数.

【答案】(1)40°;(2)18°
【解析】
(1)由∠AOC与∠BOC互余可得∠AOC+∠BOC=90°,根据角的和差关系可得∠BOD=15°,再根据角平分线的定义可得∠BOC=30°,从而得出∠AOC的度数,然后根据∠AOE=2∠EOC即可求出∠AOE的度数;
(2)设∠EOC=x,则∠AOE=2x,根据题意列方程求解即可.
解:(1)∵∠AOC与∠BOC互余,
∴∠AOC+∠BOC=90°,
即∠AOB=90°,
∵∠AOD=75°,
∴∠BOD=15°,
又∵OD平分∠BOC,
∴∠BOC=30°,
∴∠AOC=60°,
又∵∠AOE=2∠EOC,
∴![]() ;
;
(2)∠EOC=x,则
∠DOC=∠DOE﹣∠EOC=36°﹣x,
∵OD平分∠BOC,
∴∠BOC=2∠DOC=2(36°﹣x),
又∵∠AOE=2∠EOC,
∴∠AOE=2x,
∴2x+x+2(36°﹣x)=90°,
∴x=18°.
即∠EOC=18°.


科目:初中数学 来源: 题型:
【题目】观察理解,并解决问题.
问题情境:如图所示,用一些相同的小正方形,拼在一起,排成如下的一些大正方形:
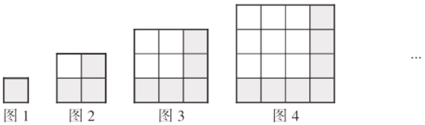
问题解决:(1)完成下表:
图序号 | 1 | 2 | 3 | 4 | … |
|
每一行小正方形的个数 | 1 | 2 | 3 | ______ | … | ______ |
阴影小正方形的个数 | 1 | 3 | 5 | ______ | … | ______ |
(2)根据图形规律推测:![]() ______(用含
______(用含![]() 的代数式表示)
的代数式表示)
(3)像(1),(2)这样,根据某类事物的部分对象具有的某种性质,推出这类事物的所有对象具有的这种性质的推理,叫做归纳推理.对于科学的发现,归纳推理是十分有用的,通过观察、实验,对有限个对象的性质作归纳整理,提出对某类事物带有规律性的猜测,是科学研究的基本方法.请观察下列等式的规律:第一个等式:![]() ;第二个等式:
;第二个等式:![]() ;第三个等式:
;第三个等式:![]() ;…猜想并直接写出第
;…猜想并直接写出第![]() 个等式.(用含
个等式.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB,点C在直线AB上,D为线段BC的中点.
(1)若AB=8 ,AC=2,求线段CD的长.
![]()
(2)若点E是线段AC的中点,直接写出线段DE和AB的数量关系是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:O是直线AB上一点,∠AOC=50°,OD是∠BOC的角平分线,OE⊥OC于点O.求∠DOE的度数.(请补全下面的解题过程)

解:∵O是直线AB上一点,∠AOC=50°,
∴∠BOC=180°-∠AOC= °.
∵ OD是∠BOC的角平分线,
∴∠COD= ∠BOC .( )
∴∠COD=65°.
∵OE⊥OC于点O,(已知).
∴∠COE= °.( )
∴∠DOE=∠COE-∠COD= ° .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数几何?”
译文:“有几个人共同出钱买鸡,如果每人出九钱,那么多了十一钱;如果每人出六钱,那么少了十六钱.问:有几个人共同出钱买鸡?设有x个人共同买鸡,根据题意列一元一次方程._____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 城气象台测得台风中心在
城气象台测得台风中心在![]() 城正西方向
城正西方向![]() 的
的![]() 处,以每小时
处,以每小时![]() 的速度向南偏东
的速度向南偏东![]() 的
的![]() 方向移动,距台风中心
方向移动,距台风中心![]() 的范围内是受台风影响的区域.
的范围内是受台风影响的区域.

(1)求![]() 城与台风中心之间的最小距离;(2)求
城与台风中心之间的最小距离;(2)求![]() 城受台风影响的时间有多长?
城受台风影响的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,江阴实验中学初三研究性学习小组要测量学校旗杆AB的高度,首先在初三楼一楼C 处测得旗杆顶部的仰角为60°,然后在初三楼三楼D处测得旗杆顶部的仰角为30°,已知旗杆底部与教学楼一楼在同一水平线上,若CD=8米,求旗杆AB的高度.
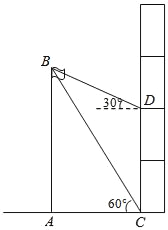
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O 为坐标原点,P、Q 是反比例函数![]() (x>0)图象上的两点,过点 P、Q 分别作直线且与 x、y 轴分别交于点 A、B和点 M、N.已知点 P 为线段 AB 的中点.
(x>0)图象上的两点,过点 P、Q 分别作直线且与 x、y 轴分别交于点 A、B和点 M、N.已知点 P 为线段 AB 的中点.
(1)求△AOB 的面积(结果用含 a 的代数式表示);
(2)当点 Q 为线段 MN 的中点时,小菲同学连结 AN,MB 后发现此时直线 AN 与直线MB 平行,问小菲同学发现的结论正确吗?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com