
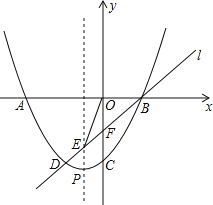
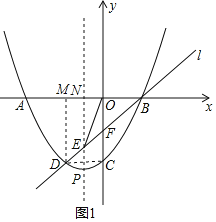
����Ŀ����ͼ����֪���κ���y��ax2+2ax+c��a��0����ͼ��x����A��B���㣬��y���ڵ�C������B��ֱ��l��������κ�����ͼ�����һ������ΪD�����ͼ��ĶԳ��ύ�ڵ�E����y�ύ�ڵ�F����DE��EF��FB��1��1��2��
��1����֤����FΪOC���е㣻
��2������OE������OBE�����Ϊ2����������κ����Ĺ�ϵʽ��
��3����������κ�����ͼ��Ķ���ΪP���ʣ���DFΪֱ����Բ�Ƿ����ǡ�þ�����P�������ܣ��������ʱ���κ����Ĺ�ϵʽ���������ܣ���˵�����ɣ�
���𰸡���1������������2��![]() ����3����DFΪֱ����Բ�ܹ�ǡ�þ�����P��
����3����DFΪֱ����Բ�ܹ�ǡ�þ�����P��![]()
��������
��1�����ȵó��Գ��ᣬ�ٱ�ʾ��D��C�����꣬������ȫ�������ε��ж������ó���DCF�ա�BOF����������𰸣�
��2�����ȵó�F�����꣬�������ô���ϵ�������ֱ��BC�Ľ���ʽ�������ó��𰸣�
��3���ɣ�1���ɵ�F��0��![]() ����E����1��
����E����1��![]() ����������EP��DE�������ó�����a��c�ĵ�ʽ����������𰸣�
����������EP��DE�������ó�����a��c�ĵ�ʽ����������𰸣�
��1����ͼ1������D��DM��FO��
��y��ax2+2ax+c��a��x+1��2+c��a��
�����ĶԳ���Ϊx����1��
��DE��EF��FB��1��1��2����DM��NE��OF��
��B��2��0������D��ĺ�����Ϊ��2��
�ɴ˿ɵ�D����2��c����
�ߵ�C��0��c����
��D��C����x����1�Գƣ�
�ʡ�DCF��90����
����DCF����BOF��
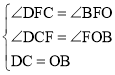
���DCF�ա�BOF��
��OF��CF��
����FΪCO���е㣮
��2���ߡ�OBE�����Ϊ2��B��2��0����
��E����1����2����
��OF��NE��
���BOF�ס�BNE��
��![]()
��![]()
��ã�FO��![]() ��
��
�ɴ˿ɵ�F��0����![]() ����C��0����
����C��0����![]() ����
����
��B��2��0����C��0����![]() ������y��ax2+2ax+c��
������y��ax2+2ax+c��
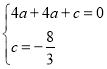
��ã� 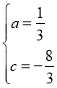
�������߽���ʽΪ�� ![]()
��3����DFΪֱ����Բ�ܹ�ǡ�þ�����P��
�ɣ�1���ɵ�F��0��![]() ����E����1��
����E����1��![]() ����D����2��c����
����D����2��c����
��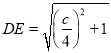
Ҫʹ��DFΪֱ����Բǡ�þ�����P����EP��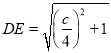
��E����1��![]() ����P����1��c��a����
����P����1��c��a����
��EP��![]()
��
��һ���棬��B��2��0���ɵ�8a+c��0����c����8a��
����������ʽ�ɵ�a��![]() ��
��
��![]()


 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
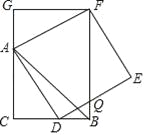
����Ŀ����ͼ��CB=CA����ACB=90�㣬��D�ڱ�BC�ϣ���B��C���غϣ����ı���ADEFΪ�����Σ�����F��FG��CA����CA���ӳ����ڵ�G������FB����DE�ڵ�Q���������½��ۣ���AC=FG����S��FAB��S�ı���CBFG=1��2���ۡ�ABC=��ABF����AD2=FQAC��������ȷ�Ľ��۵ĸ�����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
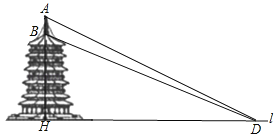
����Ŀ����ͼ��һ������AH�ĸ�Ϊ33�ף�AH��ֱ��l��ijУ���꼶��ѧ��ȤС��Ϊ�˲�øù�����ɲAB�ĸߣ���ֱ��l��ѡȡ�˵�D����D����õ�A������Ϊ26.6�㣬��õ�B������Ϊ22.8�㣬��ù�����ɲAB�ĸߣ�����ȷ��0.1�ף�(�ο����ݣ�sin26.6�㣽0.45��cos26.6�㣽0.89��tan26.6�㣽0.5��sin22.8�㣽0.39��cos22.8�㣽092��tan22.8�㣽0.42)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
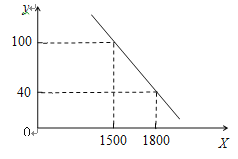
����Ŀ���̳�����һ�����ÿ������������ɱ�Ϊ1200Ԫ/̨�������鷢�֣����ֿ���������ÿ�ܵ�������y��̨�����ۼ�x��Ԫ/̨��֮��Ĺ�ϵ��ͼ��ʾ��
��1����д�����ֿ���������ÿ�ܵ�������y�� �ۼ�x�ĺ�����ϵʽ����д�Ա����ķ�Χ����
��2��������������ÿ�ܵ���������ΪW��Ԫ�������ۼ�Ϊ����ʱ���ɻ���������ʱ����������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼֱ��a��b����ֱ��m��ֱ������ֱ�ΪM��N��MN��1������ֱ����ABC��б�ߣ�AB��ֱ��m�ϣ�AB��2���ҵ�Bλ�ڵ�M����������ֱ����ABC��ֱ��m����ƽ�ƣ�ֱ����A���N�غ�Ϊֹ���ǵ�Bƽ��ƽ�Ƶľ���Ϊx������ֱ����ABC�ı�λ��ֱ��a��b֮�䲿�ֵij��Ⱥ�Ϊy����y����x�ĺ���ͼ�����Ϊ��������
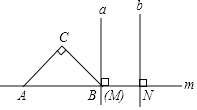
A. 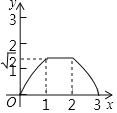 B.
B. 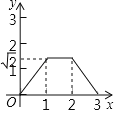
C. 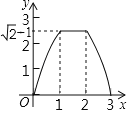 D.
D. 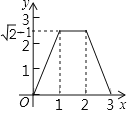
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʮ����У���������������ݱ�Ľ��У���У���꼶��֯1500��ѧ���μ���һ������һ��У֪ʶ�����������������в���ѧ���ijɼ���������60�֣�Ϊ�˸��õ��˽Ȿ�δ����ijɼ��ֲ�����������ȡ������������ѧ���ijɼ���Ϊ�������ɼ����£�
90��92��81��82��78��95��86��88��72��66��62��68��89��86��93��97��100��73��76��80��77��81��86��89��82��85��71��68��74��98��90��97��100��84��87��73��65��92��96��60��
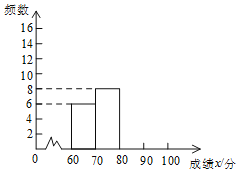
�������ɼ��������������õ����в�������ͳ��ͼ����
�ɼ�x/�� | Ƶ�� | Ƶ�� |
60��x��70 | 6 | 0.15 |
70��x��80 | 8 | 0.2 |
80��x��90 | a | b |
90��x��100 | c | d |
�����������Ϣ������������⣺
��1��a���� ����b���� ����c���� ����d���� ����
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3�����ɼ���90�����ϣ�����90�֣���Ϊ�������ȣ�������Ʋμ���α�����1500��ѧ���гɼ��������ȵ�Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
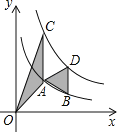
����Ŀ����ͼ����A��B�ڷ���������y��![]() (x��0)��ͼ���ϣ���C��D�ڷ���������y��
(x��0)��ͼ���ϣ���C��D�ڷ���������y��![]() (k��0)��ͼ���ϣ�AC��BD��y�ᣬ��֪��A��B�ĺ�����ֱ�Ϊ1��2����OAC���ABD�����֮��Ϊ
(k��0)��ͼ���ϣ�AC��BD��y�ᣬ��֪��A��B�ĺ�����ֱ�Ϊ1��2����OAC���ABD�����֮��Ϊ![]() ����k��ֵΪ_____��
����k��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
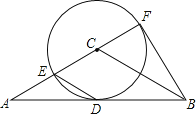
����Ŀ����ͼ������ABC�У�AC��BC��AB�ǡ�C�����ߣ��е�Ϊ��D��ֱ��AC����C�ڵ�E��F����CF=![]() AC��
AC��
��1����֤����ABF��ֱ�������Σ�
��2����AC��6����ֱ�ӻش�BF�ij��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ĵ�����װ�г���ɫ���������ͬ��5��С�����к���3������ΪA1��A2��A3��������2������ΪB1��B2����
��1�����ȴӴ���ȡ��m��m��0���������ٴӴ������������1��������������Ϊ�¼�A����գ�����AΪ��Ȼ�¼�����m��ֵΪ ����AΪ����¼�����m��ȡֵΪ
��2�����Ӵ����������2�������ú������1��������״ͼ���б���������¼��ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com