
【题目】△ABC中,AB=AC,∠BAC=30°,△ABC的面积为49,P为直线BC上一点,PE⊥AB,PF⊥AC,CH⊥AB,垂足分别为E,F,H.若PF=3,则PE=________
【答案】4或10
【解析】
连接AP.先根据三角形的面积公式分别表示出S△ABP,S△ACP,S△ABC,再由S△ABP=S△ACP+S△ABC即可得出PE=PF+PH,先根据直角三角形的性质得出AC=2CH,再由△ABC的面积为49,求出CH=7,由于CH>PF,则可分两种情况进行讨论:①P为底边BC上一点,运用结论PE+PF=CH,P为BC延长线上的点时,运用结论PE=PF+CH.
∵PE⊥AB,PF⊥AC,CH⊥AB,
∴![]()
∵S△ABP=S△ACP+S△ABC,
∴![]()
又∵AB=AC,
∴PE=PF+CH,
∵在△ACH中,∠A=30°,
∴AC=2CH,
∵![]()
∴12×2CHCH=49,
∴CH=7,
分两种情况:
①P为底边BC上一点,如图①,
∵PE+PF=CH,
∴PE=CHPF=73=4;
②P为BC延长线上的点时,如图②,
∵PE=PF+CH,
∴PE=3+7=10.
故答案为:4或10.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点选择180°得到抛物线y=x2+5x+6,则原抛物线的解析式是( )
A.y=﹣(x﹣ ![]() )2﹣
)2﹣ ![]()
B.y=﹣(x+ ![]() )2﹣
)2﹣ ![]()
C.y=﹣(x﹣ ![]() )2﹣
)2﹣ ![]()
D.y=﹣(x+ ![]() )2+
)2+ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=ax+b和反比例函数y= ![]() 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( ) 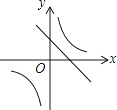
A.
B.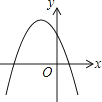
C.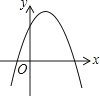
D.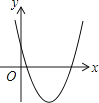
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( ) 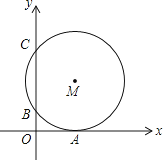
A.10
B.8 ![]()
C.4 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乐平街上新开张了一家“好又多”超市,这个星期天,张明和妈妈去这家新开张的超市买东西,如图反映了张明从家到超市的时间t(分钟)与距离s(米)之间关系的一幅图:①图中反映了哪两个变量之间的关系?超市离家多远?②张明从家出发到达超市用了多少时间?从超市返回家花了多少时间?
③张明从家出发后20分钟到30分钟内可能在做什么?④张明从家到超市时的平均速度是多少?返回时的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宜宾市某化工厂,现有A种原料52千克,B种原料64千克,现用这些原料生产甲、乙两种产品共20件.已知生产1件甲种产品需要A种原料3千克,B种原料2千克;生产1件乙种产品需要A种原料2千克,B种原料4千克,则生产方案的种数为( )
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线E:y2=4x的准线为l,焦点为F,O为坐标原点.
(1)求过点O,F,且与l相切的圆的方程;
(2)过F的直线交抛物线E于A,B两点,A关于x轴的对称点为A′,求证:直线A′B过定点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f (x)=Asin(ωx+φ),(0<φ<π)的图象如图所示,若f(x0)=3,x0∈( ![]() ,
, ![]() ),则sinx0的值为( )
),则sinx0的值为( ) 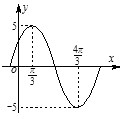
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com