
【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,点O是BC的中点,如果点M、N分别在线段AB、AC上移动,并在移动过程中始终保持AN=BM.
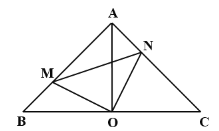
(1)求证:△ANO≌△BMO;
(2)求证:OM⊥ON.
科目:初中数学 来源: 题型:
【题目】某进口专营店销售一种“特产”,其成本价是20元/千克,根据以往的销售情况描出销量y(千克/天)与售价x(元/千克)的关系,如图所示.
(1)试求出y与x之间的一个函数关系式;
(2)利用(1)的结论:
①求每千克售价为多少元时,每天可以获得最大的销售利润.
②进口产品检验、运输等过程需耗时5天,该“特产”最长的保存期为一个月(30天),若售价不低于30元/千克,则一次进货最多只能多少千克?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 y ax2 2a(x a<0)位于 x 轴上方的图象记为F1,它与 x 轴交于 P1、O 两点,图象 F2与F1关于原点 O 对称, F2 与 x 轴的另一个交点为 P2 , F1 将与 F2 同时沿 x 轴向右平移 P1 P2 的长度即可得到F3与F4 ;再将 F3与F4 同时沿 x 轴向右平移 P1 P2 的长度即可得到 F5与F6 ;…;按这样的方式一直平移下去即可得到一系列图象 F1,F2,,Fn .我们把这组图象称为“波浪抛物线”.
(1)当 a=﹣1 时,
①求 F1 图象的顶点坐标;
②点 H(2014,﹣3) (填“在”或“不在”)该“波浪抛物线”上;若图象 F n的顶点 T n的横坐标为201,则图象 F n对应的解析式为 , 其自变量 x 的取值范围为 .
(2)设图象 Fn、Fn+1 的顶点分别为 Tn、Tn+1 (n 为正整数),x 轴上一点 Q 的坐标为(12,0).试探究: 当 a 为何值时,以 O、 Tn、Tn+1 、Q 四点为顶点的四边形为矩形?并直接写出此时 n 的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,某乘客乘高速列车从甲地经过乙地到丙地,假设列车匀速行驶.如图②表示列车离乙地路程y(千米)与列车从甲出发后行驶时间x(小时)之间的函数关系图像.
(1)甲、丙两地间的路程为千米;
(2)求高速列车离乙地的路程y与行驶时间x之间的函数关系式,并写出x的取值范围;
(3)当行驶时间x在什么范围时,高速列车离乙地的路程不超过100千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲车从A地到B地,乙车从B地到A地,乙车先出发先到达,甲乙两车之间的距离y(千米)与行驶的时间x(小时)的函数关系如图所示,则下列说法中不正确的是( )
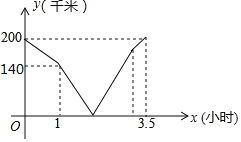
A.甲车的速度是80km/hB.乙车的速度是60km/h
C.甲车出发1h与乙车相遇D.乙车到达目的地时甲车离 B地10km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.

(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF.

(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;②当AE= cm时,四边形CEDF是菱形.(直接写出答案,不需要说明理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com