
【题目】如图①所示,某乘客乘高速列车从甲地经过乙地到丙地,假设列车匀速行驶.如图②表示列车离乙地路程y(千米)与列车从甲出发后行驶时间x(小时)之间的函数关系图像.
(1)甲、丙两地间的路程为千米;
(2)求高速列车离乙地的路程y与行驶时间x之间的函数关系式,并写出x的取值范围;
(3)当行驶时间x在什么范围时,高速列车离乙地的路程不超过100千米.

【答案】(1)1050千米;(2)当0<x<3时,y=-300x+900;当3<x<3.5时,y=300x-900;(3)当3≤x≤![]() 时,高速列车离乙地的路程不超过100千米.
时,高速列车离乙地的路程不超过100千米.
【解析】
(1)由图②可知,甲地到乙地距离900km,乙地与丙地距离150km,再由图①即可确定甲、丙两地间的距离;
(2)先确定列车到达丙地的时间,然后再用待定系数法分别求出从甲到乙、从乙到丙时,y与x的函数关系式,再根据图②确定自变量的取值范围;
(3)根据题意需分两种情况:①未到乙地时,离乙地的路程不超过100千米;②已过乙地,离乙地的路程不超过100千米,然后再分别列出不等式求出x的范围即可.
解:(1)根据图像可得,当x=0时y=900,即甲、乙两地的距离为900千米,
当x=3时,y=0,表示3小时后列车到达乙地,故列车速度为:900÷3=300千米/小时,
∵150÷300=0.5小时,
∴0.5小时后列车到达丙地,即乙丙间的距离为150千米,
故甲、丙两地间的距离为:900+150=1050千米;
(2)当0<x<3时,设函数关系式为:y=k1x+b1,
将(0,900),(3,0)代入得: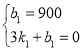
解得: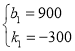
∴y=-300x+900
由于列车从甲到乙用时3小时,从乙到丙用时0.5小时,则表示乙到丙段时,3<x<3.5
故当3<x<3.5时,设函数关系式为:y=k2x+b2.
将(3,0),(3.5,150)代入得:
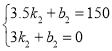 解得:
解得: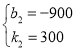
∴y=300x-900;
综上,当0<x<3时,y=-300x+900;当3<x<3.5时,y=300x-900;
(3)①当列车从甲到乙地的路程不超过100千米时,即
当0≤x≤3时有:-300x+900≤100,解得:![]() ≤x≤3;
≤x≤3;
@当列车从乙行驶到丙,到乙地的路程不超过100千米时,即
当3<x<3.5时有:300x-900≤100,解得:3≤x≤![]() ;
;
综上,当3≤x≤![]() 时,高速列车离乙地的路程不超过100千米
时,高速列车离乙地的路程不超过100千米


科目:初中数学 来源: 题型:
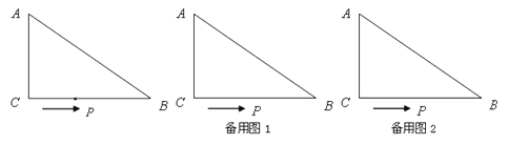
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发沿
点出发沿![]() 边向
边向![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从
从![]() 点出发沿
点出发沿![]() 向
向![]() 点以
点以![]() 的速度移动,当其中一个点到达终点时两个点同时停止运动,在两个点运动过程中,请回答:
的速度移动,当其中一个点到达终点时两个点同时停止运动,在两个点运动过程中,请回答:
![]() 经过多少时间,
经过多少时间,![]() 的面积是
的面积是![]() ?
?
![]() 请你利用配方法,求出经过多少时间,四边形
请你利用配方法,求出经过多少时间,四边形![]() 面积最小?并求出这个最小值.
面积最小?并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
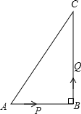
【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒.
(1)当t=1时,求△ACP的面积.
(2)t为何值时,线段AP是∠CAB的平分线?
(3)请利用备用图2继续探索:当t为何值时,△ACP是以AC为腰的等腰三角形?(直接写出结论)
(4)当p点在AB上运动时,线段CP值为整数的点有_______________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,点O是BC的中点,如果点M、N分别在线段AB、AC上移动,并在移动过程中始终保持AN=BM.
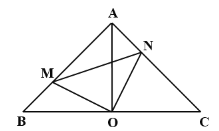
(1)求证:△ANO≌△BMO;
(2)求证:OM⊥ON.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
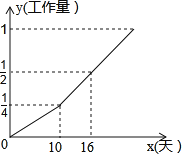
【题目】甲、乙两个工程队完成某项工程,先由甲单独做10天,乙队再加入合作.工进度满足如图所示.
(1)求工作量y与工作时间x(天)之间的函数关系式;
(2)这项工程全部完成需要多少天?
(3)求乙队单独完成这项工程的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
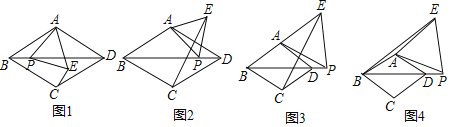
【题目】在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向右侧作等边△APE,点E的位置随点P的位置变化而变化.
(1)如图1,当点E在菱形ABCD内部或边上时,连接CE,BP与CE的数量关系是_________,CE与AD的位置关系是____________________;
(2)当点E在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由(选择图2,图3中的一种情况予以证明或说理).
(3)如图4,当点P在线段BD的延长线上时,连接BE,若![]() ,求四边形ADPE的面积.
,求四边形ADPE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com