
【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒.
(1)当t=1时,求△ACP的面积.
(2)t为何值时,线段AP是∠CAB的平分线?
(3)请利用备用图2继续探索:当t为何值时,△ACP是以AC为腰的等腰三角形?(直接写出结论)
(4)当p点在AB上运动时,线段CP值为整数的点有_______________个.
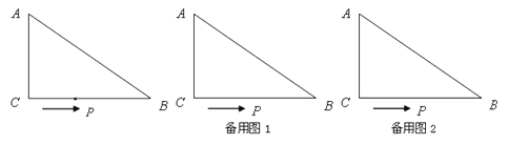
【答案】(1)6;(2)t=1.5;(3) t为3s、5.4s、6s时,△ACP为等腰三角形;(4)6
【解析】
(1)根据速度为每秒2cm,求出出发2秒后CP的长,然后根据面积公式即可得到结果;
(2)如图1,由勾股定理得到AB=![]() =10,根据已知条件得到△ACP≌△ADP,于是得到AD=AC=6cm, BD=ABAD=4cm,根据勾股定理列方程即可得到结论;
=10,根据已知条件得到△ACP≌△ADP,于是得到AD=AC=6cm, BD=ABAD=4cm,根据勾股定理列方程即可得到结论;
(3)①如图2,若P在边BC上时, AC=CP=6cm,此时用的时间为3s,△ACP为等腰三角形;②若PP在AB边上时,有两种情况: (i)若CP=AC=6cm,过C作作CD⊥AB于点D,,根据面积法求得高为4.8cm,在Rt△PCD中, PD=3.6,所以AP=2PD=7.2cm,所以PP运动的路程为187.2=10.8cm,则用的时间为5.4s,△ACP为等腰三角形;(ii)若使AP=CA=6cm,此时BP=4cm,P运动的路程为8+4=12cm,所以用的时间为6s,△ACP为等腰三角形;
(4) 当p点在AB上运动时,先求出AC的取值范围,然后分点P在点D两侧讨论即可.
解:(1)当t=1时,PC=1×2=2,
∵AC=6,
∴S△ACP=![]() ACPC=
ACPC=![]() ×6×2=6;
×6×2=6;
(2)如图,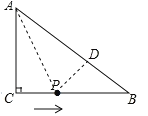
∵∠C=90°,
∴AB=![]() =10,
=10,
根据题意得:△ACP≌△ADP,
∴AD=AC=6,BD=ABAD=4,PD=PC=2t,
∴PB=82t,
在Rt△PDB中,PD2+BD2=PB2,
∴(2t)2+42=(82t)2,
解得: t=1.5;
(3)因为△ACP是以AC为腰的等腰三角形,
① 如图2,若P在边BC上时, AC=CP=6,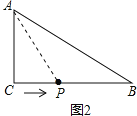
此时用的时间为t=6÷2=3,△ACP为等腰三角形;
②若P在AB边上时,有两种情况:
(i)如图3,
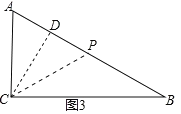
若CP=AC=6,过C作作CD⊥AB于点D,根据面积法求得高为4.8cm,
在Rt△PCD中, PD= ![]() =3.6,
=3.6,
所以AP=2PD=7.2,
所以P运动的路程为187.2=10.8,
则用的时间为t=10.8÷2=5.4,△ACP为等腰三角形;
(ii)如图4,
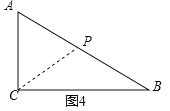
若使AP=AC=6,此时BP=4, P运动的路程为8+4=12,
所以用的时间为t=12÷2=6,△BCP为等腰三角形;
综上所述,当t为3s、5.4s、6s时,△ACP为等腰三角形.
(4)因为当p点在AB上运动时,由图3知,4.8![]() CP
CP![]() 8,
8,
当p点在DB上运动时,CP的整数值可为8,7,6,5;
当p点在DA上运动时,CP的整数值可为6,5,
综上所述,当p点在AB上运动时,线段CP值为整数的点有6个.


科目:初中数学 来源: 题型:
【题目】我们知道:x2﹣6x=(x2﹣6x+9)﹣9=(x﹣3)2﹣9;﹣x2+10=﹣(x2﹣10x+25)+25=﹣(x﹣5)2+25,这一种方法称为配方法,利用配方法请解以下各题:
(1)按上面材料提示的方法填空:a2﹣4a= = .﹣a2+12a= = .
(2)探究:当a取不同的实数时在得到的代数式a2﹣4a的值中是否存在最小值?请说明理由.
(3)应用:如图.已知线段AB=6,M是AB上的一个动点,设AM=x,以AM为一边作正方形AMND,再以MB、MN为一组邻边作长方形MBCN.问:当点M在AB上运动时,长方形MBCN的面积是否存在最大值?若存在,请求出这个最大值;否则请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以□ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E、F,延长BA交⊙A于G.

(1)求证:![]() .
.
(2)若![]() 的度数为70°,求∠C的度数.
的度数为70°,求∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:(1)(2x+y)2+(x-y)(x+y)-5x(x-y),其中x=![]() +1,y=
+1,y=![]() -1.
-1.
(2)[(x+2y)2-(x+y)(3x-5y)-5y2]÷2x,其中x=-2,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某进口专营店销售一种“特产”,其成本价是20元/千克,根据以往的销售情况描出销量y(千克/天)与售价x(元/千克)的关系,如图所示.
(1)试求出y与x之间的一个函数关系式;
(2)利用(1)的结论:
①求每千克售价为多少元时,每天可以获得最大的销售利润.
②进口产品检验、运输等过程需耗时5天,该“特产”最长的保存期为一个月(30天),若售价不低于30元/千克,则一次进货最多只能多少千克?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线![]() 经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4,则等边△AEF的边长为______.
经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4,则等边△AEF的边长为______.
 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,某乘客乘高速列车从甲地经过乙地到丙地,假设列车匀速行驶.如图②表示列车离乙地路程y(千米)与列车从甲出发后行驶时间x(小时)之间的函数关系图像.
(1)甲、丙两地间的路程为千米;
(2)求高速列车离乙地的路程y与行驶时间x之间的函数关系式,并写出x的取值范围;
(3)当行驶时间x在什么范围时,高速列车离乙地的路程不超过100千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】收发微信红包已成为各类人群进行交流联系,增强感情的一部分,下面是甜甜和她的双胞胎妹妹在六一儿童节期间的对话.
请问:(1)2015年到2017年甜甜和她妹妹在六一收到红包的年增长率是多少?
(2)2017年六一甜甜和她妹妹各收到了多少钱的微信红包?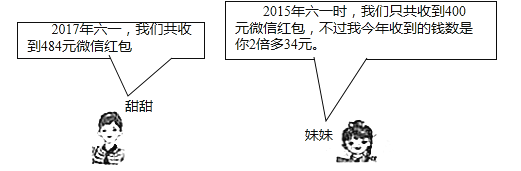
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MAN=90°,点C在边AM上,AC=4,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE并延长交A′B所在直线于点F,连接A′E.当△A′EF为直角三角形时,AB的长为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com