
 已知△ABC的边BC=8cm,高AM=6cm,长方形DEFG的一边EF落在BC上,顶点D、G分别落在AB和AC上,如果长方形的面积为12cm2,求长和宽.
已知△ABC的边BC=8cm,高AM=6cm,长方形DEFG的一边EF落在BC上,顶点D、G分别落在AB和AC上,如果长方形的面积为12cm2,求长和宽.  名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
 元;在矩形EFGH上兴建爱心鱼池,每平方米投资4元.
元;在矩形EFGH上兴建爱心鱼池,每平方米投资4元.查看答案和解析>>
科目:初中数学 来源: 题型:
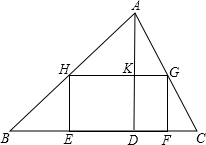
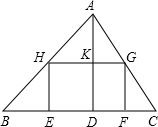 如图所示,某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造.已知△ABC的边BC长120米,高AD长80米.学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图).其中矩形EFGH的一边EF在边BC上.其中两个顶点H、G分别在边AB、AC上.现计划在△AHG上种草,在△BHE、△GFC上都种花,在矩形EFGH上兴建喷泉.当FG长为多少米时,种草的面积与种花的面积相等?
如图所示,某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造.已知△ABC的边BC长120米,高AD长80米.学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图).其中矩形EFGH的一边EF在边BC上.其中两个顶点H、G分别在边AB、AC上.现计划在△AHG上种草,在△BHE、△GFC上都种花,在矩形EFGH上兴建喷泉.当FG长为多少米时,种草的面积与种花的面积相等?查看答案和解析>>
科目:初中数学 来源: 题型:
 爱心鱼塘,每平方米投资5元,设矩形的一边FG长为x米.
爱心鱼塘,每平方米投资5元,设矩形的一边FG长为x米.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•金山区一模)如图,已知△ABC的边BC长15厘米,高AH为10厘米,长方形DEFG内接于△ABC,点E、F在边BC上,点D、G分别在边AB、AC上.
(2012•金山区一模)如图,已知△ABC的边BC长15厘米,高AH为10厘米,长方形DEFG内接于△ABC,点E、F在边BC上,点D、G分别在边AB、AC上.| AD | AB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com