
【题目】已知,△ABC是等边三角形,如图①,点D、E分别在射线BA、BC上,且AD=CE,求证:△BDE是等边三角形;

(2)如图②,点D在BA边上,点E在射线BC上,AD=CE,连接DE交AC于点F,请问DF与EF的数量关系是什么?并说明理由.
【答案】(1)见解析;(2)DF=EF,理由见解析.
【解析】
(1)利用有一个角是60度的等腰三角形是等边三角形进行判定;
(2)过点D作DH∥BE交AC于点H,证得△DHF≌△ECF(ASA),可得出DF=EF.
(1)证明:∵△ABC是等边三角形,
∴∠B =60°,AB=BC,
∵AD=CE,
∴AB+AD=BC+CE,即BD=BE,
∴△BDE是等腰三角形,
又∵∠B =60°,
∴△BDE是等边三角形;
(2)DF=EF,理由是:
如图②,过点D作DH∥BE交AC于点H,
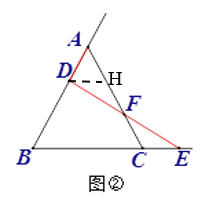
∵△ABC是等边三角形,
∴∠A=∠B =∠ACB=60°,
∵DH∥BE,
∴∠ADH=∠B =60°,∠AHD=∠ACB =60°,
∴△ADH是等边三角形,
∴AD=DH,
∵AD=CE,
∴DH=CE,
∵DH∥BE,
∴∠HDF=∠E, ∠DHF=∠FCE,
在△DHF和△ECF中,
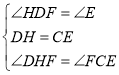
∴△DHF≌△ECF(ASA)
∴DF=EF


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中,x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 |
y | 0 | ﹣3 | ﹣4 | ﹣3 |
下列结论:
①ac<0;
②当x>1时,y随x的增大而增大;
③﹣4是方程ax2+(b﹣4)x+c=0的一个根;
④当﹣1<x<0时,ax2+(b﹣1)x+c+3>0.其中正确结论的个数为( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60 m到达点C,测得点B在点C的北偏东60°方向,如图②.
(1)求∠CBA的度数;
(2)求出这段河的宽(结果精确到1 m,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73).
≈1.73).

① ②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线a∥b,依次有3个三角形放置在上面,它们分别是等边三角形、等腰直角三角形、含30°角的直角三角形,直接填写出∠1、∠2、∠3 的度数.

∠1= °;∠2= °;∠3= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个30°的角BAC与角MON,顶点A在射线ON上某处,现保持角MON不动,将角BAC绕点A以每秒15°的速度顺时针旋转,边AB、AC分别与边OM交于点P、Q,当AC∥OM时,交点Q消失旋转结束。设运动时间为t秒(t>0).


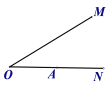

(1)当t=2秒时,OP:PQ= ;
(2)在运动的过程中,△APQ能否成为等腰三角形?若能,请利用备用图,直接写出此时的运动时间;
(3)在(2)中判断△OAQ的形状,并选择其中的一个说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于( )
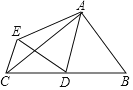
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线的顶点![]() ,且经过点
,且经过点![]() ,与
,与![]() 轴分别交于
轴分别交于![]() 两点.
两点.

(1)求直线![]() 和该抛物线的解析式;
和该抛物线的解析式;
(2)如图1,点![]() 是抛物线上的一个动点,且在直线
是抛物线上的一个动点,且在直线![]() 的上方,过点
的上方,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 交于点
交于点![]() ,求
,求![]() 的最大值;
的最大值;
(3)如图2,![]() 轴交
轴交![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上
是抛物线上![]() 、
、![]() 之间的一个动点,直线
之间的一个动点,直线![]() 、
、![]() 与
与![]() 分别交于
分别交于![]() 、
、![]() ,当点
,当点![]() 运动时,求
运动时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB![]() AC,过AB上一点D作DE∥AC交BC于点E,以E为顶点,ED为一边,作∠DEF
AC,过AB上一点D作DE∥AC交BC于点E,以E为顶点,ED为一边,作∠DEF![]() ∠A,另一边EF交AC于点F.
∠A,另一边EF交AC于点F.
(1)求证:四边形ADEF为平行四边形;
(2)当D为AB中点时,四边形ADEF的形状为 (直接写出结论);
(3)延长图1中的DE到点G,使EG![]() DE,连接AE,AG,FG,得到图2.若AD
DE,连接AE,AG,FG,得到图2.若AD![]() AG,判断四边形AEGF的形状,并说明理由.
AG,判断四边形AEGF的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com