
【题目】如图,![]() 是由
是由![]() 绕点
绕点![]() 顺时针旋转得到的,连结
顺时针旋转得到的,连结![]() 交斜边于点
交斜边于点![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() .
.
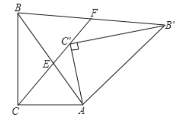
(1)若![]() ,
,![]() ,求
,求![]() ;
;
(2)证明:![]() ;
;
(3)设![]() ,试探索
,试探索![]() 满足什么关系时,
满足什么关系时,![]() 与
与![]() 是全等三角形,并说明理由.
是全等三角形,并说明理由.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() ,见解析
,见解析
【解析】
(1)根据旋转的性质可以证得:△ACC′∽△ABB′,即可求解;
(2)根据旋转的性质可以证得:AC=AC′,AB=AB′,∠CAB=∠C′AB′,再根据∠AEC=∠FEB即可证明两个三角形相似;
(3)当β=2α时,△ACE≌△FBE.易证∠ABC=∠BCE,再根据CE=BE,即可证得.
(1)解:∵AC=AC′,AB=AB′,
∴![]()
由旋转可知:∠CAB=∠C′AB′,
∴∠CAB+∠EAC′=∠C′AB′+∠EAC′,即∠CAC′=∠BAB′,
又∵∠ACB=∠AC′B′=90°,
∴△ACC′∽△ABB′,
∵AC=3,AB=4,
∴![]() ;
;
(2)证明:∵Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,
∴AC=AC′,AB=AB′,∠CAB=∠C′AB′,
∴∠CAC′=∠BAB′,
∴∠ABB′=∠AB′B=∠ACC′=∠AC′C,
∴∠ACC′=∠ABB′,
又∵∠AEC=∠FEB,
∴△ACE∽△FBE.
(3)解:当β=2α时,△ACE≌△FBE.理由:
在△ACC′中,
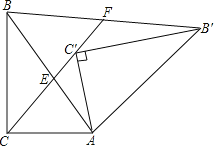
∵AC=AC′,
∴∠ACC′=∠AC′C=![]() =90°-α,
=90°-α,
在Rt△ABC中,
∠ACC′+∠BCE=90°,
即90°-α+∠BCE=90°,
∴∠BCE=90°-90°+α=α,
∵∠ABC=α,
∴∠ABC=∠BCE,
∴CE=BE,
由(2)知:△ACE∽△FBE,
∴△ACE≌△FBE.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】已知函数y=(2m+1)x+m﹣3;
(1)若函数图象经过原点,求m的值;
(2)若函数图象在y轴的截距为﹣2,求m的值;
(3)若函数的图象平行直线y=3x﹣3,求m的值;
(4)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
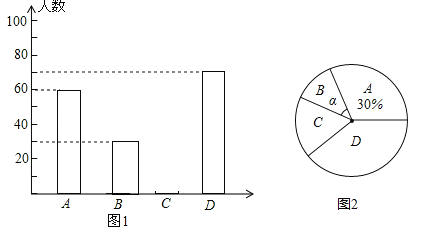
【题目】黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题:
(1)本次抽样调查共抽取了多少名学生?并将条形统计图补充完整;
(2)本次抽样调查中,学习时间的中位数落在哪个等级内?
(3)表示B等级的扇形圆心角α的度数是多少?
(4)在此次问卷调查中,甲班有2人平均每天课外学习时间超过2小时,乙班有3人平均每天课外学习时间超过2小时,若从这5人中任选2人去参加座谈,试用列表或化树状图的方法求选出的2人来自不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
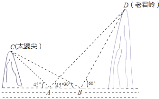
【题目】在一次暑假旅游中,小亮在仙岛湖的游船上(A处),测得湖西岸的山峰太婆尖(C处)和湖东岸的山峰老君岭(D处)的仰角都是45°.游船向东航行100米后(B处),测得太婆尖,老君岭的仰角分别为30°,60°.试问太婆尖、老君岭的高度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
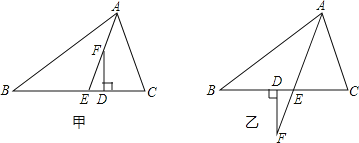
【题目】已知,如图甲,在△ABC中,AE平分∠BAC(∠C>∠B),F为AE上一点,且FD⊥BC于D.
(1)试说明:∠EFD=![]() (∠C﹣∠B);
(∠C﹣∠B);
(2)当F在AE的延长线上时,如图乙,其余条件不变,(1)中的结论还成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60,请你探究OE,EF之间有什么数量关系?并证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
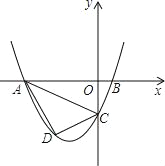
【题目】已知,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)直接写出C点的坐标;
(2)求抛物线的解析式;
(3)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
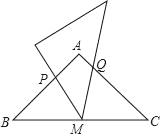
【题目】等腰直角三角形ABC中,∠BAC=90°,BC=12,点M为BC中点,含45°的直角三角板的锐角顶点与M重合,当三角板绕点M旋转时,三角板与两直角边交于点P、Q.P、Q分别在AB、AC边上,设BP=x,CQ=y.
(1)求y与x的函数关系式;
(2)写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com