
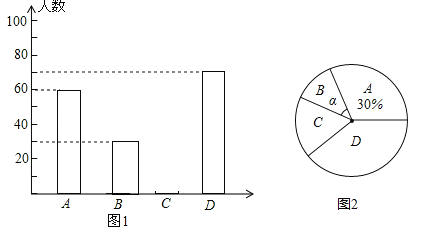
【题目】黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题:
(1)本次抽样调查共抽取了多少名学生?并将条形统计图补充完整;
(2)本次抽样调查中,学习时间的中位数落在哪个等级内?
(3)表示B等级的扇形圆心角α的度数是多少?
(4)在此次问卷调查中,甲班有2人平均每天课外学习时间超过2小时,乙班有3人平均每天课外学习时间超过2小时,若从这5人中任选2人去参加座谈,试用列表或化树状图的方法求选出的2人来自不同班级的概率.
【答案】(1)200;(2)C;(3)54°;(4)![]() .
.
【解析】
试题分析:(1)根据B类的人数和所占的百分比即可求出总数;求出C的人数从而补全统计图;
(2)根据中位数定义:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数可得答案;
(3)用B的人数除以总人数再乘以360°,即可得到圆心角α的度数;
(4)先设甲班学生为A1,A2,乙班学生为B1,B2,B3根据题意画出树形图,再根据概率公式列式计算即可.
试题解析:(1)共调查的中学生数是:80÷40%=200(人),C类的人数是:200﹣60﹣80﹣20=40(人),如图1:
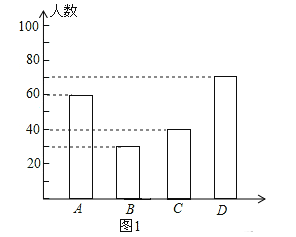
(2)本次抽样调查中,学习时间的中位数落在C等级内;
(3)根据题意得:α=![]() ×360°=54°;
×360°=54°;
(4)设甲班学生为A1,A2,乙班学生为B1,B2,B3,画树状图为:
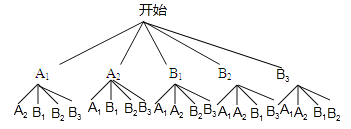
一共有20种等可能结果,其中2人来自不同班级共有12种,∴P(2人来自不同班级)=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知关于x的一次函数y=mx+2的图象经过点(﹣2,6).
(1)求m的值;
(2)画出此函数的图象;
(3)平移此函数的图象,使得它与两坐标轴所围成的图形的面积为4,请直接写出此时图象所对应的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个相似三角形对应角平分线的比为16:25,那么它们的面积比为( )
A. 4:5 B. 16:25 C. 196:225 D. 256:625
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,且a,b满足|a+2|+(b﹣1)2=0.点A与点B之间的距离表示为AB(以下类同).
(1)求AB的长;
(2)点C在数轴上对应的数为x,且x是方程2x﹣2=![]() x+2的解,在数轴上是否存在点P,使得PA+PB=PC?若存在,求出点P对应的数;若不存在,说明理由;
x+2的解,在数轴上是否存在点P,使得PA+PB=PC?若存在,求出点P对应的数;若不存在,说明理由;
(3)在(1)、(2)的条件下,点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和C分别以每秒4个单位长度和9个单位长度的速度向右运动,经过t秒后,请问:AB﹣BC的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其常数值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个相似三角形的对应边分别是15cm和23cm,它们的周长相差40cm,则这两个三角形的周长分别是( )
A. 45cm,85cm B. 60cm,100cm C. 75cm,115cm D. 85cm,125cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.形状相同的两个三角形一定全等
B.面积相等的两个三角形一定全等
C.所有的正方形都全等
D.一个图形经过平移后,前后两个图形一定全等
查看答案和解析>>
科目:初中数学 来源: 题型:
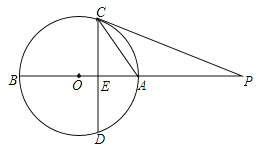
【题目】如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足为E,且![]() =PEPO.
=PEPO.
(1)求证:PC是⊙O的切线.
(2)若OE:EA=1:2,PA=6,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,正确的是( )
A.形状相同的两个三角形是全等形
B.面积相等的两个三角形全等
C.周长相等的两个三角形全等
D.周长相等的两个等边三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若多项式3x2-2xy-y2减去多项式M所得的差是-5x2+xy-2y2,则多项式M是( )
A. -2x2-xy-3y2 B. 2x2+xy+3y2 C. 8x2-3xy+y2 D. -8x2+3xy-y2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com