
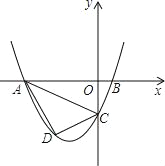
【题目】已知,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)直接写出C点的坐标;
(2)求抛物线的解析式;
(3)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
【答案】(1) (0,﹣3);(2) y=![]() x2+
x2+![]() x﹣3;(3) 四边形ABCD面积的最大值为13.5.
x﹣3;(3) 四边形ABCD面积的最大值为13.5.
【解析】
(1)由点B的坐标为(1,0),OC=3OB,且点C在y轴的负半轴上可求出点C的坐标;
(2)已知了B点坐标,易求得OB、OC的长,进而可将B、C的坐标代入抛物线中,求出待定系数的值,即可得出抛物线的解析式.
(3)根据A、C的坐标,易求得直线AC的解析式.由于AB、OC都是定值,则△ABC的面积不变,若四边形ABCD面积最大,则△ADC的面积最大;可过D作x轴的垂线,交AC于M,x轴于N;易得△ADC的面积是DM与OA积的一半,可设出N点的坐标,分别代入直线AC和抛物线的解析式中,即可求出DM的长,进而可得出四边形ABCD的面积与N点横坐标间的函数关系式,根据所得函数的性质即可求出四边形ABCD的最大面积.
(1)∵点B的坐标为(1,0),OC=3OB,
∴OB=1,OC=3,
∴点C的坐标为(0,﹣3).
(2)将B(1,0)、C(0,﹣3)代入y=ax2+3ax+c,得:
![]() ,解得:
,解得: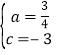 ,
,
∴抛物线的解析式为y=![]() x2+
x2+![]() x﹣3.
x﹣3.
(3)过点D作直线DE∥y轴,交AC于点E,交x轴于点F,过点C作CG⊥DE于点G,如图所示.
当y=0时,有![]() x2+
x2+![]() x﹣3=0,
x﹣3=0,
解得:x1=﹣4,x2=1,
∴点A的坐标为(﹣4,0),
∴AB=5.
设直线AC的解析式为y=kx+b(k≠0),
将A(﹣4,0)、C(0,﹣3)代入y=kx+b,得:
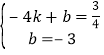 ,解得:
,解得: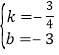 ,
,
∴直线AC的解析式为y=﹣![]() x﹣3.
x﹣3.
设点D的坐标为(t,![]() x2+
x2+![]() x﹣3),则点E的坐标为(t,﹣
x﹣3),则点E的坐标为(t,﹣![]() t﹣3),
t﹣3),
∴ED=﹣![]() t﹣3﹣(
t﹣3﹣(![]() x2+
x2+![]() x﹣3)=﹣
x﹣3)=﹣![]() t2﹣3t,
t2﹣3t,
∴S四边形ABCD=S△ABC+S△AED+S△CED,
=![]() ABOC+
ABOC+![]() EDAF+
EDAF+![]() EDCG,
EDCG,
=![]() ABOC+
ABOC+![]() EDAO,
EDAO,
=![]() ×5×3+
×5×3+![]() ×4(﹣
×4(﹣![]() t2﹣3t),
t2﹣3t),
=﹣![]() t2﹣6t+
t2﹣6t+![]() =﹣
=﹣![]() (t+2)2+
(t+2)2+![]() .
.
∵﹣![]() <0,
<0,
∴当t=﹣2时,四边形ABCD的面积取最大值,最大值为![]() .
.
答:四边形ABCD面积的最大值为![]() .
.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
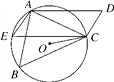
【题目】如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连接AE.
(1)求证:四边形AECD为平行四边形;
(2)连接CO,求证:CO平分∠BCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
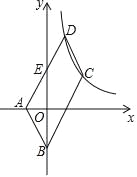
【题目】如图,平行四边形ABCD中,A(-1,0)、B(0,-2),顶点C、D在双曲线![]() (x>0)上,边AD交y轴于点E,若点E恰好是AD的中点,则k=_____.
(x>0)上,边AD交y轴于点E,若点E恰好是AD的中点,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
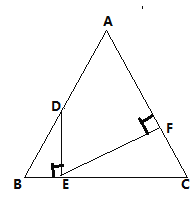
【题目】如图,等边△ABC的边长为12, D为AB边上一动点,过点D作DE⊥BC于点E.过点E作EF⊥AC于点F.
(1)若AD=2,求AF的长;
(2)当AD取何值时,DE=EF?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距72千米,李磊骑自行车往返两地一共用了7小时,已知他去时的平均速度比返回时的平均速度快![]() ,求李磊去时的平均速度是多少?
,求李磊去时的平均速度是多少?
小芸同学解法如下:
解:设李磊去时的平均速度是x千米/时,则返回时的平均速度是(1-![]() )x千米/时,由题意得:
)x千米/时,由题意得:![]() +
+![]() =7,…
=7,…
你认为小芸同学的解法正确吗?若正确,请写出该方程所依据的等量关系,并完成剩下的步骤;若不正确,请说明原因,并完整地求解问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C处测得教学楼顶部D处的仰角为18°,教学楼底部B处的俯角为20°,教学楼的高BD=21m,求实验楼与教学楼之间的距离AB(结果保留整数).(参考数据:tan18°≈0.32,tan20°≈0.36)

查看答案和解析>>
科目:初中数学 来源: 题型:
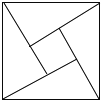
【题目】如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为![]() ,较短直角边长为
,较短直角边长为![]() ,若
,若![]() ,大正方形的面积为13,则小正方形的面积为________.
,大正方形的面积为13,则小正方形的面积为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com