
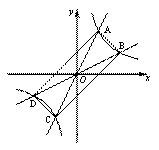
如图,过原点的直线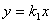 和
和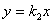 与反比例函数
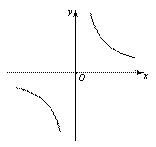
与反比例函数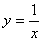 的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.
的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.
(1)四边形ABCD一定是 四边形;(直接填写结果)
(2)四边形ABCD可能是矩形吗?若可能,试求此时k1和k2之间的关系式;若不可能,说明理由;
(3)设P(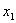 ,
,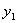 ),Q(
),Q(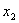 ,
,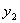 )(x2 > x1 > 0)是函数
)(x2 > x1 > 0)是函数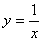 图象上的任意两点,
图象上的任意两点,
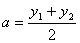 ,
, ,试判断
,试判断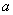 ,
,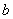 的大小关系,并说明理由.
的大小关系,并说明理由.
科目:初中数学 来源: 题型:
如图是由相同的花盆按一定的规律组成的正多边形图案,其中第1个图形一共有6个花盆,第2个图形一共有12个花盆,第3个图形一共有20个花盆,…,则第8个图形中花盆的个数为
 |
A.56 B.64 C.72 D.90
查看答案和解析>>
科目:初中数学 来源: 题型:
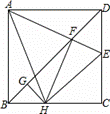
如图,在正方形ABCD中,AB=4,点E为CD上一动点,AE交BD于点F,过点F作FH⊥AE,交BC于H,过H作GH⊥BD于点G,下列结论:①AF=FH, ②∠HAE=45°, ③BD=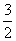 FG,④△CEH的周长为定值.其中正确的是 (写正确结论的序号)。
FG,④△CEH的周长为定值.其中正确的是 (写正确结论的序号)。
查看答案和解析>>
科目:初中数学 来源: 题型:
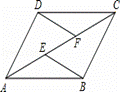
如图,E,F是四边形ABCD对角线AC上的两点,AD∥BC ,DF∥BE ,AE=CF.
求证:(1)△AFD≌△CEB;(2)四边形ABCD是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com