
【题目】如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连接CD,过点B作BG丄CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连接DF.给出以下四个结论:
①![]() ; ②点F是GE的中点; ③AF=
; ②点F是GE的中点; ③AF=![]() AB;④S△ABC=5S△BDF,其中正确的结论序号是__________.
AB;④S△ABC=5S△BDF,其中正确的结论序号是__________.

【答案】①③
【解析】试题分析:∵在Rt△ABC中,∠ABC=90°,∴AB⊥BC,AG⊥AB,∴AG∥BC,∴△AFG∽△CFB,
∴![]() ,∵BA=BC,∴
,∵BA=BC,∴![]() ,故①正确;∵∠ABC=90°,BG⊥CD∴∠DBE+∠BDE=∠BDE+∠BCD=90°,
,故①正确;∵∠ABC=90°,BG⊥CD∴∠DBE+∠BDE=∠BDE+∠BCD=90°,
∴∠DBE=∠BCD,∵AB=CB,点D是AB的中点,∴BD=![]() AB=
AB=![]() CB,∵tan∠BCD=
CB,∵tan∠BCD=![]() =
=![]() ,∴在Rt△ABG中,tan∠DBE=
,∴在Rt△ABG中,tan∠DBE=![]() =
=![]() ,∵
,∵![]() ,∴FG=
,∴FG=![]() FB,故②错误;∵△AFG∽△CFB,∴AF:CF=AG:BC=1:2,
FB,故②错误;∵△AFG∽△CFB,∴AF:CF=AG:BC=1:2,
∴AF=![]() AC,∵AC=
AC,∵AC=![]() AB,∴AF=
AB,∴AF=![]() AB,故③正确;∵BD=
AB,故③正确;∵BD=![]() AB,AF=
AB,AF=![]() AC,∴S△ABC=6S△BDF,故④错误.故答案为:①③.
AC,∴S△ABC=6S△BDF,故④错误.故答案为:①③.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】动漫节开幕前,某动漫公司预测某种动漫玩具能够畅销,就分两批分别用32000元和68000元购进了这种玩具销售,其中第二批购进数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该动漫公司这两批各购进多少套玩具?
(2)如果这两批玩具每套售价相同,且全部销售后总利润不少于20000元,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,属于真命题的是( )
A.各边相等的多边形是正多边形
B.矩形的对角线互相垂直
C.三角形的中位线把三角形分成面积相等的两部分
D.对顶角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
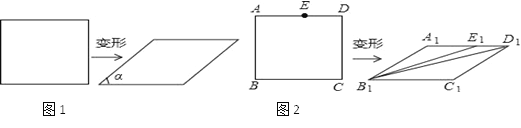
我们知道,四边形具有不稳定性,容易变形,如图1,一个矩形发生变形后成为一个平行四边形,设这个平行四边形相邻两个内角中较小的一个内角为α,我们把![]() 的值叫做这个平行四边形的变形度.
的值叫做这个平行四边形的变形度.
(1)若矩形发生变形后的平行四边形有一个内角是120度,则这个平行四边形的变形是 .
猜想证明:
(2)设矩形的面积为S1,其变形后的平行四边形面积为S2,试猜想S1,S2, ![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
拓展探究:
(3)如图2,在矩形ABCD中,E是AD边上的一点,且AB2=AEAD,这个矩形发生变形后为平行四边形A1B1C1D1,E1为E的对应点,连接B1E1,B1D1,若矩形ABCD的面积为4![]() (m>0),平行四边形A1B1C1D1的面积为2
(m>0),平行四边形A1B1C1D1的面积为2![]() (m>0),试求∠A1E1B1+∠A1D1B1的度数.
(m>0),试求∠A1E1B1+∠A1D1B1的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果仅用一种正多边形进行镶嵌,下列正多边形:正五边形、正方形、正六边形、正八边形、正三角形中不能构成平面镶嵌的有( )个.
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w (千克)与销售价x (元/千克)有如下关系:w=﹣2x+80.设这种产品每天的销售利润为y (元).
(1)求y与x之间的函数关系式,自变量x的取值范围;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
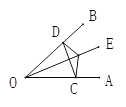
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
求证:(1)∠ECD=∠EDC;
(2)OC=OD;
(3)OE是线段CD的垂直平分线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com