
【题目】认真阅读下面的材料,完成有关问题:
材料 在学习绝对值时,老师教过我们绝对值的几何含义,如|5-3|表示5,3在数轴上对应的两点之间的距离;|5+3|=|5-(-3)|,所以|5+3|表示5,-3在数轴上对应的两点之间的距离;|5|=|5-0|,所以|5|表示5在数轴上对应的点到原点的距离.一般地,点A,B在数轴上分别表示有理数a,b,那么A,B之间的距离可表示为|a-b|.
(1)点A,B,C在数轴上分别表示有理数-5,-1, 3,那么A到B的距离是 ,A到C的距离是_____.(直接填最后结果)
(2)点A,B,C在数轴上分别表示有理数x,-2,1,那么A到B的距离与A到C的距离之和可表示为 (用含绝对值的式子表示).
(3)利用数轴探究:
①设|x-3|+|x+1|=p,当x的值取在不小于-1 且不大于3的范围时,p的值是不变的,而且是p的最小值,这个最小值是_____;
②求|x|+|x-2|的最小值以及此时x的取值范围?
【答案】(1)4,8; (2)|x+2|+|x-1|或|x-(-2)|+|x-1|;(3)①4;②当x的取值在不小于0且不大于2的范围时,|x|+|x-2|的最小值是2.
【解析】
(1)根据两点间距离公式代入相应的值即可得出答案;
(2)根据两点间距离公式分别求出A到B的距离和A到C的距离,两式相加即可得出答案;
(3)①根据“x的值取在不小于-1 且不大于3的范围”将绝对值化简再进行计算即可得出答案;②根据①中的探究可知,当x的取值在不小于0且不大于2的范围时,|x|+|x-2|有最小值,再根据x的取值范围化简绝对值,即可得出最小值.
解:(1)A到B的距离是:![]() ;
;
A到C的距离是:![]() ;
;
(2)A到B的距离是:![]() ;
;
A到C的距离是:![]()
∴A到B的距离与A到C的距离之和可表示为:![]() ;
;
(3)①∵x的值取在不小于-1 且不大于3的范围
∴![]()
又|x-3|+|x+1|=p
∴p=4,这个最小值是4;
②∵当x的值取在不小于-1 且不大于3的范围时,|x-3|+|x+1|有最小值,最小值为4
∴当x的取值在不小于0且不大于2的范围时,|x|+|x-2|有最小值,最小值为2.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】一儿童服装商店在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六·一”儿童节,商店决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装上盈利1200元,那么每件童装应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
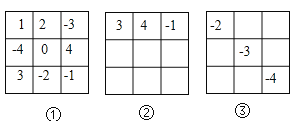
【题目】如图的图例①是一个方阵图,每行的3个数、每列的3个数、斜对角的3个数相加的和均相等.如果将方阵图的每个数都加上同一个数,那么方阵中每行的3个数、每列的3个数、斜对角的3个数相加的和仍然相等,这样就形成新的方阵图.
根据图①②③中给出的数,对照原来的方阵图,请你完成图②③的方阵图?
查看答案和解析>>
科目:初中数学 来源: 题型:
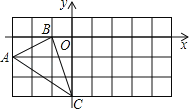
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣3,﹣1)、B(﹣1,0)、C(0,﹣3)
(1)点A关于坐标原点O对称的点的坐标为 .
(2)将△ABC绕点C顺时针旋转90°,画出旋转后得到的△A1B1C,A1A的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小华骑自行车从家出发到植物园玩,从家出发 1 小时后,因自行车损坏修理了一段时间后,按原速前往植物园,小华从家出发 1 小时 50 分后,爸爸从家出发骑摩托车沿相同路线前往植物园,如图是他们家的路程 y(km)与小华离家的时间 x(h)的函数图象,已知爸爸骑摩托车的速度是小华骑车速度的 2 倍,若爸爸比小华早 10 分达到植物园,则小华家到植物园的路程是_____km.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 13×7 的网格中,每个小正方形边长都是 1,其顶点叫做格点,如图 A、B、D、E 均为格点,![]() ABD 为格点三角形.
ABD 为格点三角形.

(1)请在给定的网格中画 ABCD,要求 C 点在格点上;
(2)在(1)中 ABCD 右侧,以格点 E 为其中的一个顶点,画格点![]() EFG,并使 EF=5,FG=3,EG=
EFG,并使 EF=5,FG=3,EG=![]()
(3)先将(2)中的线段 EF 向右平移 6 个单位、再向下平移 l 个单位到 MP 的位置,再以 MP 为对角线画矩形 MNPQ(M、N、P、Q 按逆时针方向排列),直接写出矩形 MNPQ 的面积为 ______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E为AD上一点,FG⊥CE分别交AB、CD于F、G,垂足为O.
(1)求证:CE=FG;
(2)如图2,连接OB,若AD=3DE,∠OBC=2∠DCE。
求![]() 的值;
的值;
若AD=3,则OE的长为_________(直接写出结果).


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六(2)班同学准备春游,某品牌牛奶每盒200毫升,售价2元.
(1)在甲商店购买,买5盒送一盒;在乙商场购买,九折优惠.全班42人,要给每位同学准备一瓶这样的牛奶,该去哪家商场购买比较合算?为什么?
(2)商店提供装牛奶的是一个长方体纸箱,下面是它的展开图,请算出这个长方体纸箱的表面积.(黏贴处不算,单位:分米)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com