
【题目】如图,矩形ABCD中,AB=10,BC=5,点P为AB边上一动点(不与点A,B重合),DP交AC于点Q.
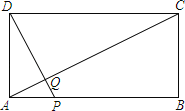
(1)求证:△APQ∽△CDQ;
(2)当PD⊥AC时,求线段PA的长度;
(3)当点P在线段AC的垂直平分线上时,求sin∠CPB的值.
【答案】(1)见解析;(2)AP=![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)根据矩形的性质和相似三角形的判定定理证明即可;
(2)根据垂直的定义、相似三角形的性质列出比例式,计算即可;
(3)连接PC,根据线段垂直平分线的性质得到PC=PA,设PA=x,根据勾股定理列出关于x的方程,解方程即可.
(1)证明:∵四边形ABCD是矩形,
∴DC∥AB,
∴∠QAP=∠QCD,∠QPA=∠QDC,
∴△APQ∽△CDQ;
(2)解:∵PD⊥AC,
∴∠QDC+∠QCD=90°,又∠QDC+∠QDA=90°,
∴∠QCD=∠QDA,又∠DAP=∠CDA=90°,
∴△DAP∽△CDA,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,AP=![]() ;
;
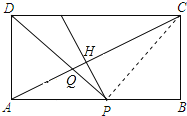
(3)解:连接PC,
∵点P在线段AC的垂直平分线上,
∴PC=PA,
设PA=x,则PC=x,PB=10﹣x,
由勾股定理得,PC2=PB2+BC2,即x2=(10﹣x)2+25,
解得,x=![]() ,
,
∴PC=PA=![]() ,
,
∴sin∠CPB=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() 与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).
与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).
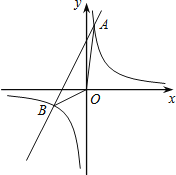
(1)求k1、k2、b的值;
(2)求△AOB的面积;
(3)若M(x1,y1)、N(x2,y2)是反比例函数y=![]() 图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限,并简要说明理由.
图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() 与一次函数y=k2x+b图象的交点为A(m,1),B(﹣2,n),OA与x轴正方向的夹角为α,且tanα=
与一次函数y=k2x+b图象的交点为A(m,1),B(﹣2,n),OA与x轴正方向的夹角为α,且tanα=![]() .
.
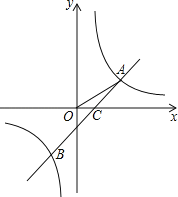
(1)求反比例函数及一次函数的表达式;
(2)设直线AB与x轴交于点C,且AC与x轴正方向的夹角为β,求tanβ的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
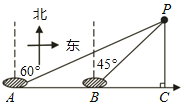
【题目】如图,点P表示我国的钓鱼岛,在此岛周围25海里水域有暗礁.我渔政海监船由西向东航行到A处,发现P岛在北偏东60°的方向上,轮船继续向前航行20海里到达B处,发现P岛在北偏东45°的方向上.该船若不改变航向继续前进,有无触礁的危险?(参考数据![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?

已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
探究四:若将上题中的四边形ABCD改为六边形ABCDEF(图4)呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,A、B、C、D四点共圆,过点C的切线CE∥BD,与AB的延长线交于点E.
(1)求证:∠BAC=∠CAD;
(2)如图②,若AB为⊙O的直径,AD=6,AB=10,求CE的长;
(3)在(2)的条件下,连接BC,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com