
【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?

已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
探究四:若将上题中的四边形ABCD改为六边形ABCDEF(图4)呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系: .
【答案】探究一:∠FDC+∠ECD =180°+∠A;探究二:∠DPC=90°+![]() ∠A;探究三:∠PDC==
∠A;探究三:∠PDC==![]() (∠A+∠B);探究四:∠P=
(∠A+∠B);探究四:∠P=![]() (∠A+∠B+∠E+∠F)﹣180°
(∠A+∠B+∠E+∠F)﹣180°
【解析】试题分析:探究一:根据三角形的一个外角等于与它不相邻的两个内角的和可得∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,再根据三角形内角和定理整理即可得解;
探究二:根据角平分线的定义可得∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,然后根据三角形内角和定理列式整理即可得解;
∠ACD,然后根据三角形内角和定理列式整理即可得解;
探究三:根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理探究二解答即可;
探究四:根据六边形的内角和公式表示出∠ADC+∠BCD,然后同理探究二解答即可.
解:探究一:∵∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,
∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A;
探究二:∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,
∠ACD,
∴∠DPC=180°﹣∠PDC﹣∠PCD,
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠ACD,
∠ACD,
=180°﹣![]() (∠ADC+∠ACD),
(∠ADC+∠ACD),
=180°﹣![]() (180°﹣∠A),
(180°﹣∠A),
=90°+![]() ∠A;
∠A;
探究三:∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠BCD,
∠BCD,
∴∠DPC=180°﹣∠PDC﹣∠PCD,
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠BCD,
∠BCD,
=180°﹣![]() (∠ADC+∠BCD),
(∠ADC+∠BCD),
=180°﹣![]() (360°﹣∠A﹣∠B),
(360°﹣∠A﹣∠B),
=![]() (∠A+∠B);
(∠A+∠B);
探究四:六边形ABCDEF的内角和为:(6﹣2)180°=720°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠P=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,
∠ACD,
∴∠P=180°﹣∠PDC﹣∠PCD,
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠ACD,
∠ACD,
=180°﹣![]() (∠ADC+∠ACD),
(∠ADC+∠ACD),
=180°﹣![]() (720°﹣∠A﹣∠B﹣∠E﹣∠F),
(720°﹣∠A﹣∠B﹣∠E﹣∠F),
=![]() (∠A+∠B+∠E+∠F)﹣180°,
(∠A+∠B+∠E+∠F)﹣180°,
即∠P=![]() (∠A+∠B+∠E+∠F)﹣180°.
(∠A+∠B+∠E+∠F)﹣180°.


科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=4,BC=3,以点D为圆心作圆,使A、B、C三点中至少有一点在圆内且至少一点在圆外,⊙O的的半径r的取值范围是_________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AB=10cm,sinA=![]() .如果点P由B出发沿BA向点A匀速运动,同时点Q由A出发沿AC向点C匀速运动.已知点P的速度为2cm/s,点Q的速度为1cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤5)
.如果点P由B出发沿BA向点A匀速运动,同时点Q由A出发沿AC向点C匀速运动.已知点P的速度为2cm/s,点Q的速度为1cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤5)

(1)求AC,BC的长;
(2)当t为何值时,△APQ的面积为△ABC面积的![]() ;
;
(3)当t为何值时,△APQ与△ABC相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=10,BC=5,点P为AB边上一动点(不与点A,B重合),DP交AC于点Q.
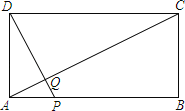
(1)求证:△APQ∽△CDQ;
(2)当PD⊥AC时,求线段PA的长度;
(3)当点P在线段AC的垂直平分线上时,求sin∠CPB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE。
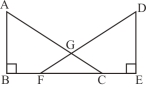
求证:(1)△ABC≌△DEF;
(2)GF=GC。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】氢原子中电子和原子核之间的距离为0.00000000529厘米,用科学记数法表示这个距离为( )
A. 5.29×10-8 cm ; B. 5.29×10-9cm; C. 0.529×10-8 cm; D. 52.9×10-10 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地相距40千米,中午12:00时,甲从A地出发开车到B地,12:10时乙从B地出发骑自行车到A地,设甲行驶的时间为t(分),甲、乙两人离A地的距离S(千米)与时间t(分)之间的关系如图所示.由图中的信息可知,乙到达A地的时间为( )
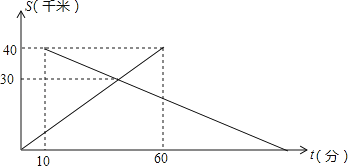
A.14:00 B.14:20 C.14:30 D.14:40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
①a、b同号;
②当x=1和x=3时,函数值相等;
③4a+b=0;
④当y=﹣2时,x的值只能取0.
其中正确的个数是( )
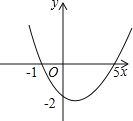
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com