
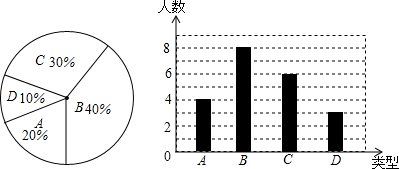
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
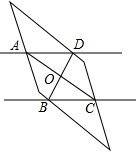 如图,一把宽为$\sqrt{3}$cm的直尺放在一个边长为2$\sqrt{3}$cm,一顶角为30°的菱形纸片上,尺子边缘与菱形纸片相交于点A,B,C,D,连接AC,BD它们相交于点O,则∠AOD的度数为75°.
如图,一把宽为$\sqrt{3}$cm的直尺放在一个边长为2$\sqrt{3}$cm,一顶角为30°的菱形纸片上,尺子边缘与菱形纸片相交于点A,B,C,D,连接AC,BD它们相交于点O,则∠AOD的度数为75°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
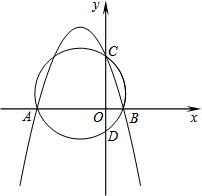 如图,抛物线y=-$\frac{3}{4}$x2-$\frac{9}{4}$x+3与x轴交于点A、B,与y轴交于点C.经过A、B、C三点的圆与y轴的负半轴交于点D.
如图,抛物线y=-$\frac{3}{4}$x2-$\frac{9}{4}$x+3与x轴交于点A、B,与y轴交于点C.经过A、B、C三点的圆与y轴的负半轴交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
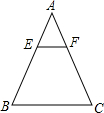 如图,在△ABC中,EF∥BC,$\frac{AE}{EB}$=$\frac{1}{3}$,S四边形BCFE=15,则S△ABC=16.
如图,在△ABC中,EF∥BC,$\frac{AE}{EB}$=$\frac{1}{3}$,S四边形BCFE=15,则S△ABC=16.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com