
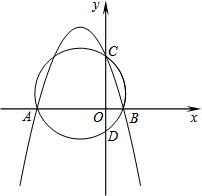 如图,抛物线y=-$\frac{3}{4}$x2-$\frac{9}{4}$x+3与x轴交于点A、B,与y轴交于点C.经过A、B、C三点的圆与y轴的负半轴交于点D.
如图,抛物线y=-$\frac{3}{4}$x2-$\frac{9}{4}$x+3与x轴交于点A、B,与y轴交于点C.经过A、B、C三点的圆与y轴的负半轴交于点D.分析 (1)把x=0,y=0分别代入抛物线y=-$\frac{3}{4}$x2-$\frac{9}{4}$x+3,解方程即可求出A、B、C三点的坐标;
(2)存在,如图1,连接AD,BC,求得A与D的坐标,设直线AD的解析式为y=kx+b,利用待定系数法即可求得直线AD的解析式,则可求得此时点P的坐标;
(3)由(1)和(2)可知A(-4,0),B(1,0),C(0,3),D(0,-$\frac{4}{3}$),进而可求出圆心的坐标为Q(-$\frac{3}{2}$,$\frac{5}{6}$),再分两种情况:若PQ为平行四边形的边和若PQ为平行四边形的对角线分别讨论即可求出符合条件的E点坐标.
解答 解:
(1)∵当x=0时,y=3,
∴C(0,3),
∵当y=0时,-$\frac{3}{4}$x2-$\frac{9}{4}$x+3=0,
解得x=-4或1,
∴A(-4,0),B(1,0);
(2)存在一点P使得PB+PD的值最小,理由如下:
如图1,连接AD,BC.
∵圆经过A、B、C、D四点,
∴∠ADO=∠CBO,
∵∠AOD=∠COB=90°,
∴△AOD∽△COB,
∴$\frac{OD}{OA}=\frac{OB}{OC}$,
由题意知,AO=4,BO=1,CO=3,
∴OD=$\frac{4}{3}$,
∴D(0,-$\frac{4}{3}$),
设AD的解析式为y=kx+b,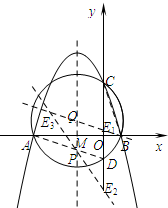
将A(-4,0),D(0,-$\frac{4}{3}$)代入解得
k=-$\frac{1}{3}$,b=-$\frac{4}{3}$,
∴y=-$\frac{1}{3}$,x-$\frac{4}{3}$,
由题意知,抛物线对称轴为x=-$\frac{3}{2}$
∵A、B关于x=-$\frac{3}{2}$对称,
∴当x=-$\frac{3}{2}$时,y=-$\frac{5}{6}$,即P(-$\frac{3}{2}$,-$\frac{5}{6}$)时,PB+PD=PA+PD=PD最短.
(3)由(1)可知A(-4,0),B(1,0),C(0,3),
由(2)可知D(0,-$\frac{4}{3}$),
∴圆心的坐标为Q(-$\frac{3}{2}$,$\frac{5}{6}$),
∴PQ=$\frac{5}{3}$,
若PQ为平行四边形的边,
∵PQ∥y轴,PQ=DE,
∴OE=$\frac{1}{3}$或3,
∴E1(0,$\frac{1}{3}$)或者E2(0,-3),
若PQ为平行四边形的对角线,
PQ的中点坐标为M(-$\frac{3}{2}$,0),
∴E3(-3,$\frac{4}{3}$).
综上可知以D、E、P、Q为顶点的四边形为平行四边形时所有符合条件的E点坐标为(0,$\frac{1}{3}$)或(0,-3)或(-3,$\frac{4}{3}$).
点评 本题主要考查了二次函数的综合性题目,用到的知识点有:利用待定系数法求函数的解析式,函数和坐标轴的交点问题,相似三角形的判定和性质以及线段和最短问题等知识.此题综合性较强,难度较大,解题的关键是利用分类讨论与数形结合思想的灵活运用.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
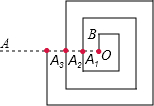 如图是一回形图,其回形通道的宽和OB的长均为1,回形线与射线OA交于A1、A2、A3….若从O点到A1点的回形线为第1圈(长为7),从A1点到A2点的回形线为第2圈,从A2点到A3点的回形线为第3圈,…,依此类推,则第10圈的长为79.
如图是一回形图,其回形通道的宽和OB的长均为1,回形线与射线OA交于A1、A2、A3….若从O点到A1点的回形线为第1圈(长为7),从A1点到A2点的回形线为第2圈,从A2点到A3点的回形线为第3圈,…,依此类推,则第10圈的长为79.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com