
已知:如图,Rt△ABC中,∠ACB=90°°,AC=3,BC=4.
(1)求AB的长;
(2)在直线AC、BC上分别取一点M、N,使得△AMN≌△ABN,求CN的长.

考点: 勾股定理;全等三角形的判定.
分析: (1)由勾股定理求出AB即可;
(2)分两种情况:①当∠BAN=∠MAN,且AM=AB时,则BN=MN,且AM=AB=5,求出CM,设CN=x,在Rt△MCN中,由勾股定理得出方程,解方程即可;
②当∠BAN=∠MAN,且AM=AB时,则BN=MN,且AM=AB=5,求出CM=8,设CN=x,则BN=MN=x+4,在Rt△MCN中,由勾股定理得出方程,解方程即可.
解答: 解:(1)∵∠ACB=90°,AC=3,BC=4,
∴AB=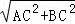 =
=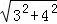 =5;
=5;
(2)分两种情况:
①如图1所示:
当∠BAN=∠MAN,且AM=AB时,有△AMN≌△ABN,
则BN=MN,且AM=AB=5,
∴CM=2,
设CN=x,
在Rt△MCN中,MC2+CN2=MN2,
即22+x2=(4﹣x)2,
解得:x=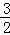 ,
,
∴CN=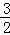 ;
;
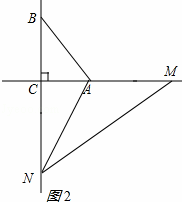
②如图2所示:
当∠BAN=∠MAN,且AM=AB时,有△AMN≌△ABN,
则BN=MN,且AM=AB=5,
∴CM=8,
设CN=x,则BN=MN=x+4,
在Rt△MCN中,MC2+CN2=MN2,
即82+x2=(4+x)2,
解得:x=6,
∴CN=6;
综上所述:CN的长为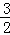 或6.
或6.
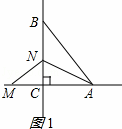


科目:初中数学 来源: 题型:
如图,将一块面积为30m2的正方形铁皮的四个角各截去一个面积为2m2的小正方形,剩下的部分刚好能围成一个无盖的长方体运输箱,求此运输箱底面的边长.(精确到0.1m)

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,AB=AC,且D为BC上一点,CD=AD,AB=BD,则∠B的度数为( )
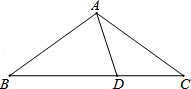
A. 30° B. 36° C. 40° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法:①若a、b互为相反数,则a+b=0;②若a+b=0,则a、b互为相反数;③若a、b互为相反数,则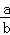 =﹣1; ④若
=﹣1; ④若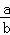 =﹣1,则a、b互为相反数.其中正确的结论有( )
=﹣1,则a、b互为相反数.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com